Rette vinkler og Pythagoras
Hvis en tømrer ved en fejl kommer til at skrue et bræt skævt på en konstruktion, kan han forholdsvis ubesværet skrue det fri igen og rette det op, hvorefter han kan fastgøre brættet rigtigt. Hvis derimod en murer kommer til at mure en hel mur skæv, kræver det ofte et enormt stykke arbejde at rive muren ned, for derefter at opføre den igen. Derfor er det vigtigt, at man inden for murerfaget benytter sig af nogle teknikker, der kan sikre, at de mure, som man opfører, har de rigtige vinkler hele vejen igennem opmuringsprocessen.
Hvis en murer gerne vil opføre en mur, der står vinkelret på en anden mur, som står der i forvejen, hvordan kan hun så sikre sig at den nye mur danner en 90 graders vinkel, og bliver muret lige ud fra denne vinkel?

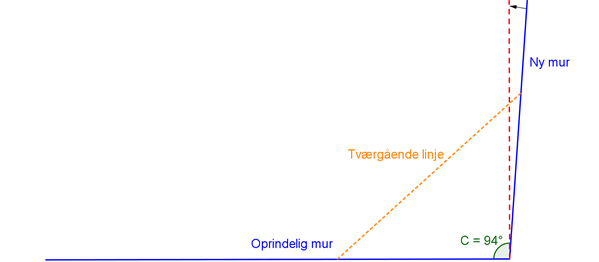
Det første man kunne komme i tanke om at gøre, er at bruge en vinkelmåler til at opmåle en vinkel på 90\(^{\circ}\) ud fra den mur, der står der i forvejen, og så ellers lave en sigtelinje (med tape, snor, kridt eller lignende), som den nye mur skal mures efter. Problemet med denne fremgangsmåde er, at hvis man kommer til at opmåle den vinkel, der skulle være 90 \(^{\circ}\), forkert, fx til 94 \(^{\circ}\), så bliver den nye mur skæv. Jo længere den nye mur skal være, jo mere bliver muren påvirket af den lille opmålingsfejl, hvilket er vist på tegningen herunder.

Tegningen forestiller situationen set oppefra. Den blå vandrette linje er den oprindelige mur, mens den anden blå linje er den nye mur, der skal bygges. Hvis mureren ved en fejl er kommet til at opmåle en vinkel på 94 \(^{\circ}\)i stedet for 90 \(^{\circ}\), bliver den nye mur skæv i forhold til, hvor den egentlig skulle have været (den røde stiplede linje). Jo længere den nye mur skal være, jo mere kommer den til at afvige fra den stiplede linje.
Selvom mureren bruger en vinkelmåler til at opmåle den vinkel, der skal være 90 \(^{\circ}\), kan det nemt ske, at hun kommer til at måle forkert. For at undgå at den nye mur bliver skæv, kan hun under opmuringen gøre brug af den matematiske viden, hun har fra Pythagoras' læresætning.
Pythagoras' læresætning fortæller, at i en retvinklet trekant, hvor \(a\), \(b\) og \(c\) betegner længden af trekantens sider, så gælder der, at
$$a^2+b^2=c^2.$$

Men det er faktisk en anden formulering af Pythagoras' læresætning som mureren kan drage nytte af. Der gælder nemlig også, at hvis en trekants sidelængder, \(a\), \(b\) og \(c\), opfylder at \(a^2+b^2=c^2\), så er trekanten en retvinklet trekant. Mureren kan bruge dette ved at forbinde den oprindelige mur og den nye mur med en tværgående linje, så der skabes en trekant bestående af den oprindelige mur, den nye mur og den tværgående linje. Ved at måle hvor lange siderne i denne opståede trekant er, og tjekke, om de opfylder, at \(a^2+b^2=c^2\), ved mureren, om vinklen mellem den oprindelige mur og den nye mur, er 90 \(^{\circ}\).
Tegningen forestiller situationen set oppefra.
Eksempler
Eksempel 1:
En murer har fået til opgave at bygge en mur ud fra en anden mur, der står der i forvejen, således at de to mure danner en ret vinkel.
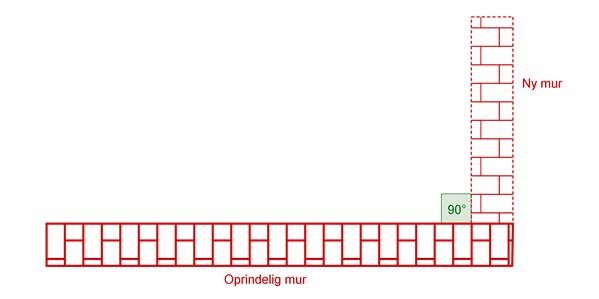
Tegningen forestiller situationen set oppefra. Mureren bruger en vinkelmåler til at afmåle, hvad hun mener er \(90^{\circ}\). Efter at havet muret de første 3 meter af den nye mur, gør mureren et holdt, for at tjekke om vinklen egentlig er \(90^{\circ}\), og om hun dermed er på rette kurs. Hun anskaffer sig en bjælke, som hun med sikkerhed ved er 5 meter lang. Denne bjælke lægger hun således, at den ene af bjælkens ender rører, der hvor hun er nået til med den nye mur, og den anden af bjælkens ender rører 4 meter ude af den oprindelige mur (se tegningen nedenfor). Denne bjælke udgør nu den tværgående linje, som hun skal bruge til at tjekke, om vinklen er \(90^{\circ}\).
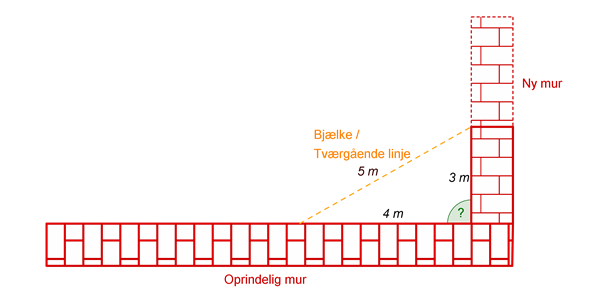
Tegningen forestiller situationen set oppefra. For at den grønne vinkel er \(90^{\circ}\), skal der ifølge Pythagoras' læresætning gælde, at
$$a^2+b^2=c^2,$$
hvilket i dette tilfælde svarer til, at der skal gælde, at
$$3^2+4^2=5^2.$$
For at finde ud af om \(3^2+4^2\) er lig med \(5^2\), udregner vi dem hver for sig, og ser om det giver det samme.
$$3^2+4^2=(3\cdot3)+(4\cdot4)=9+16=25.$$
$$5^2=5\cdot5=25.$$
Da begge udtryk giver det samme, ved vi at Pythagoras' læresætning er opfyldt, og vi kan derfor konkludere, at vinklen rent faktisk er \(90^{\circ}\). Mureren kan dermed roligt fortsætte. Skulle mureren senere hen igen blive i tvivl, om hun måske er begyndt at mure skævt, kan hun foretage samme tjek.
Eksempel 2:
Vi kigger igen på eksemplet ovenfor med mureren, der skal bygge en ny mur, således at den står vinkelret ud fra en anden mur, der står der i forvejen. Efter at havet muret de første 3 meter af den nye mur, gør mureren et holdt, for at tjekke om vinklen egentlig er \(90^{\circ}\), og om hun dermed er på rette kurs. Hun anskaffer sig en bjælke, som hun med sikkerhed ved er 5 meter lang. Denne bjælke lægger hun således, at den ene af bjælkens ender rører, der hvor hun er nået til med den nye mur, og den anden af bjælkens ender rører den oprindelige mur. Hun kan måle at bjælkens anden ende rører 3,75 meter ude af den oprindelige mur (se tegningen nedenfor).
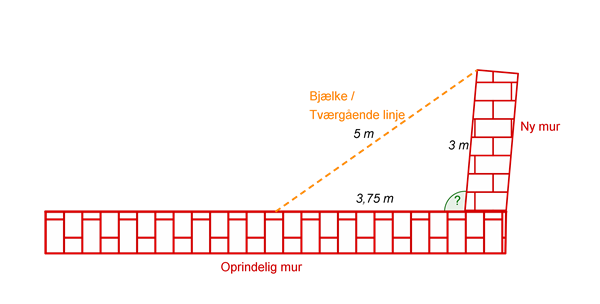
Tegningen forestiller situationen set oppefra. For at den grønne vinkel er \(90^{\circ}\), skal der ifølge Pythagoras' læresætning gælde, at
$$a^2+b^2=c^2,$$
hvilket i dette tilfælde svarer til, at der skal gælde, at
$$3^2+(3,75)^2=5^2.$$
For at finde ud af om \(3^2+(3,75)^2\) er lig med \(5^2\), udregner vi dem hver for sig, og ser om det giver det samme.
$$3^2+(3,75)^2=(3\cdot3)+(3,75\cdot3,75)=9+14,06=23,06.$$
$$5^2=5\cdot5=25.$$
Da de to udtryk ikke giver det samme, ved vi at Pythagoras' læresætning ikke er opfyldt, og vi kan derfor konkludere, at vinklen faktisk ikke er \(90^{\circ}\). Mureren har derfor opmuret den nye mur skævt, og hun bliver nødt til at rive den ned og starte forfra, hvis hun vil have det ønskede resultat. Heldigvis for mureren havde hun ikke færdiggjort den nye mur, men blot påbegyndt den, inden hun foretog tjekket. Havde hun muret den nye mur helt færdig, inden tjekket blev foretaget, havde rettearbejdet været betydelig mere omfattende.
