Potensfunktioner

Den tredje vigtige type funktion (udover lineære og eksponentielle) er potensfunktionerne.

Et eksempel på en potensfunktion kunne være

$$y=5\cdot x^2$$

Og den generelle forskrift for en potensfunktion er

$$y=b\cdot x^a$$

Den hedder en potensfunktion, fordi den består af en potens (x^a) med fast eksponent (a) og variabelt grundtal (x). Derudover er der en koefficient, b, der ganges på.

Potensfunktionen har den egenskab, at når x-værdien stiger med en fast procent, så stiger y-værdien også med en fast procent. Under tiden kaldes potensfunktioner også procent-procent-vækst.

Det betyder med andre ord, at når vi ganger vores x-værdi med et tal, k, så skal vi gange vores y-værdi med k^a.

Læg mærke til, hvordan det adskiller sig fra eksponentialfunktionen, hvor y steg med en vis procent, når x steg med et tal. I potensvæksten skal x stige med en procent og ikke et tal, før y stiger med en bestemt procent.

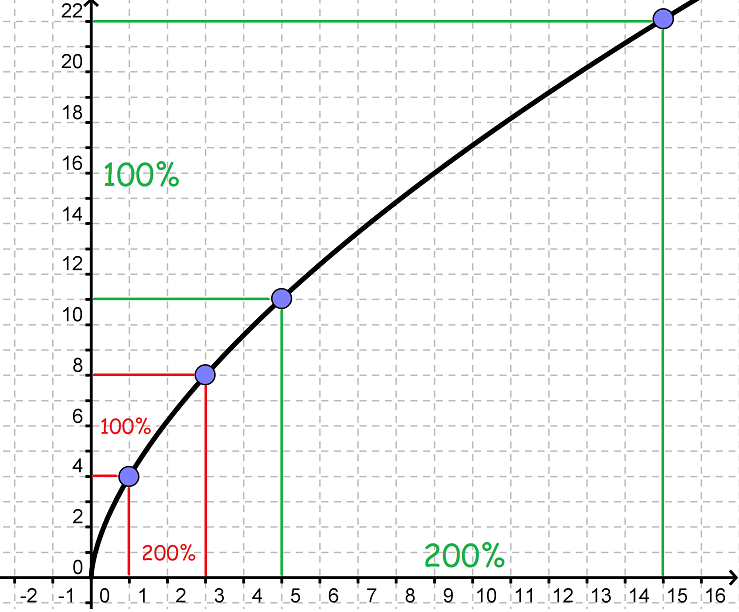
Vi kan se på grafen, at når x vokser med 200% (dvs. vi ganger med 3), så vokser y med 100% (dvs. vi ganger med 2).

Når x=1, og vi stiger 200%, er vi oppe på 3. Og y er steget med 100% (fra 4 til 8)

Når x=5, og vi stiger med 200%, er vi oppe på 15. Og y er steget med 100% (fra 11 til 22).

Lige meget hvor vi starter, vil en forøgelse på 200% på x-aksen resultere i, at y forøges med 100%.

Man kan også udtrykke det på en anden måde.

Hvis vi fremskriver en x-værdi med faktoren F_x så fremskrives y-værdien med faktoren F_y, og sammenhængen mellem de to faktorer er

$$F_y={F_x}^a\quad\Leftrightarrow\quad F_x=\sqrt[a]{F_y}$$

Hvis vi f.eks. har potensfunktionen

$$y=5x^2$$

og vil fremskrive vores x-værdi med 20 % (Dvs F_x=1,20), så er

$$F_y={F_x}^a=1,20^2=1,44$$

Dvs. at når x stiger med 20% så vil y stige med 44%

Hvis vi gerne vil have y til at stige med 69 % (dvs. F_y=1,69), hvor mange procent skal vores x så fremskrives?

$$F_x=\sqrt[a]{F_y}=\sqrt[2]{1,69}=\sqrt{1,69}=1,30$$

Dvs. når y stiger med 69 % så stiger x med 30%.

Betydningen af a

I modsætning til de to andre funktionstyper, kan grafen for potensfunktioner se meget forskellige ud. Udseendet afhænger i høj grad af, hvilken værdi a har.

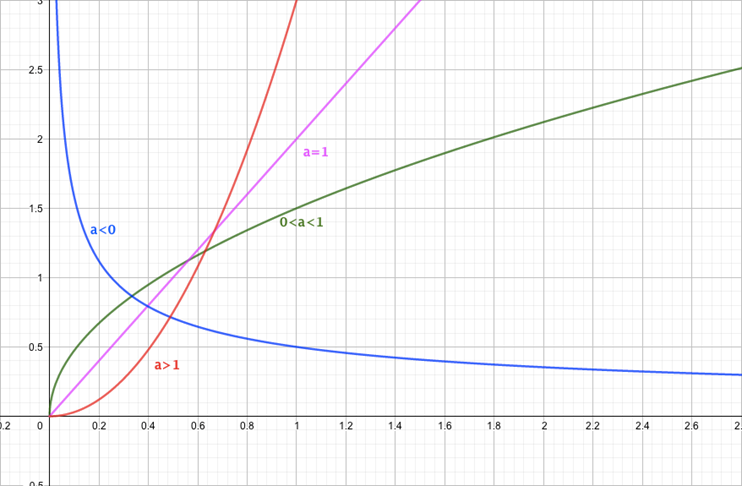
Vi ser, at hvis a er mindre end 0, vil grafen starte højt oppe og smyge sig ned langs y-aksen for så at nærme sig 0 og så smyge sig henad x-aksen. Bemærk, at den aldrig krydser nogen af akserne! Funktionen er altså aftagende.

Hvis a er 0, er funktionen konstant med y=b.

Hvis a ligger mellem 0 og 1, vil vi have en voksende graf, som flader mere og mere ud. 

Hvis a er 1, har vi en ret linje (med hældning b). Og sidst men ikke mindst: hvis a er større end 1, har vi en graf, der vokser og bliver mere og mere stejl.

Når a ligger mellem 0 og 1, er potensfunktionen faktisk også en "rodfunktion". Som eks. Er

$$x^\frac{1}{2}=\sqrt{x}$$

(se evt. afsnittet om kvadratrødder og andre rødder).

Derfor vil en funktion som

$$y=5x^\frac{1}{3}$$

være det samme som

$$y=5\cdot\sqrt[3]{x}$$

Betydning af b

Ovenfor har vi set, hvad tallet a betyder for grafens udseende.

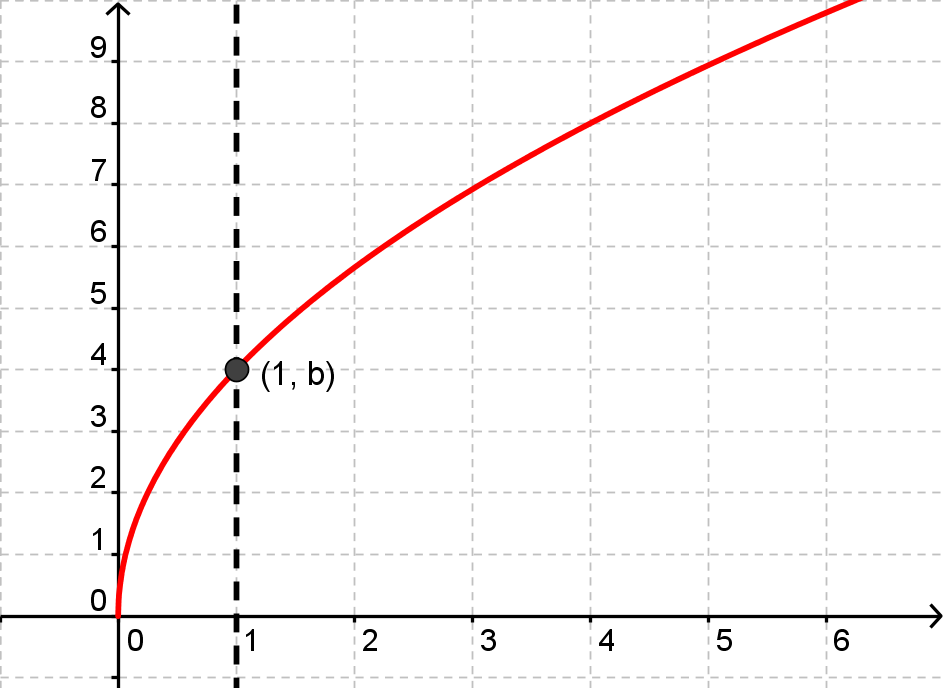
Imidlertid siger tallet b også noget om, hvordan grafen ser ud. Det er nemlig den værdi, der er på y-aksen, når x er 1. For at aflæse b ud fra en graf skal man altså gå ud ad x-aksen til man støder på 1, og derefter gå op ad y-aksen, til man støder på grafen; y-værdien i dette punkt er så b.

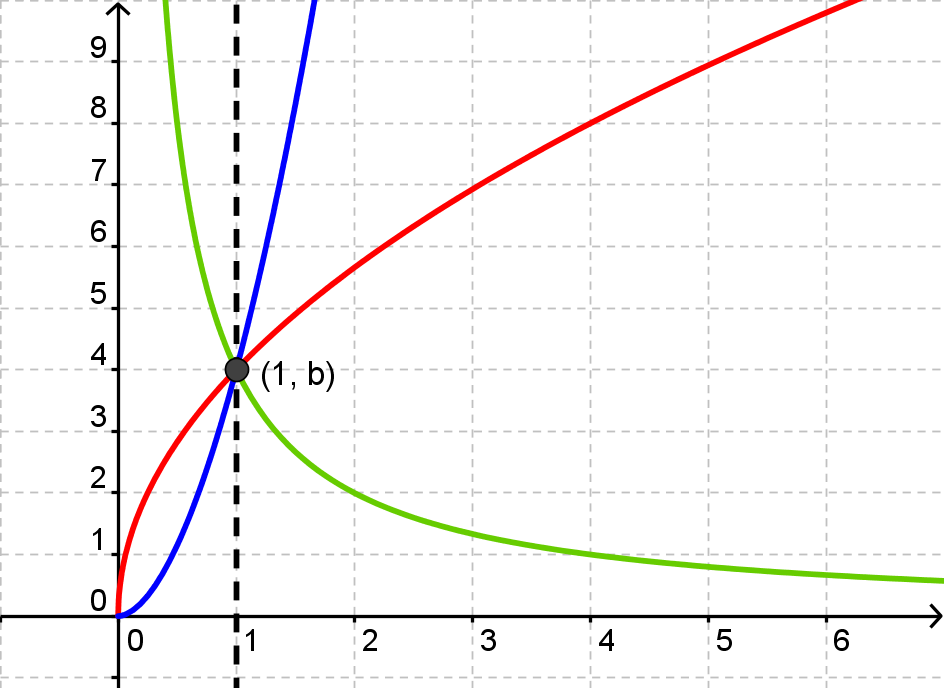
Her ser vi forskellige potensfunktioner med samme b-værdi (men vidt forskellige a-værdier).

Grafen

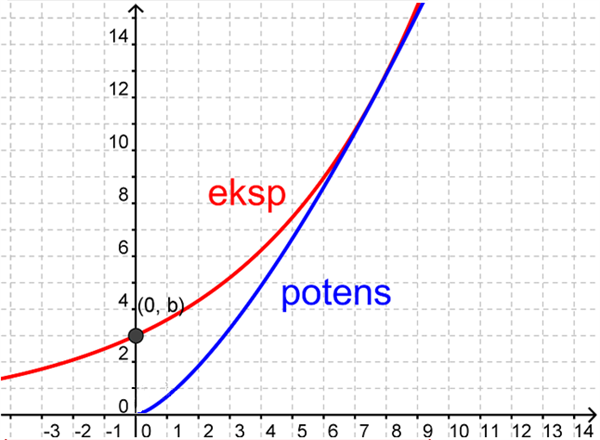
Nogle gange kan grafen for en potensfunktion ligne grafen for en eksponentiel funktion til forveksling. Imidlertid er der nogle tommelfingerregler, så man kan kende forskel.

Når a er større end 1, ligner grafer en voksende eksponentialfunktion. Der hvor de adskiller sig er, at grafen for en eksponentialfunktion vil skære y-aksen i punktet (0,b), mens potensfunktionens graf kommer uendeligt tæt på origo (0,0), men aldrig helt vil skære y-aksen (selvom det på grafen ser sådan ud), fordi potensfunktionen kun er defineret for positivie reelle tal. 

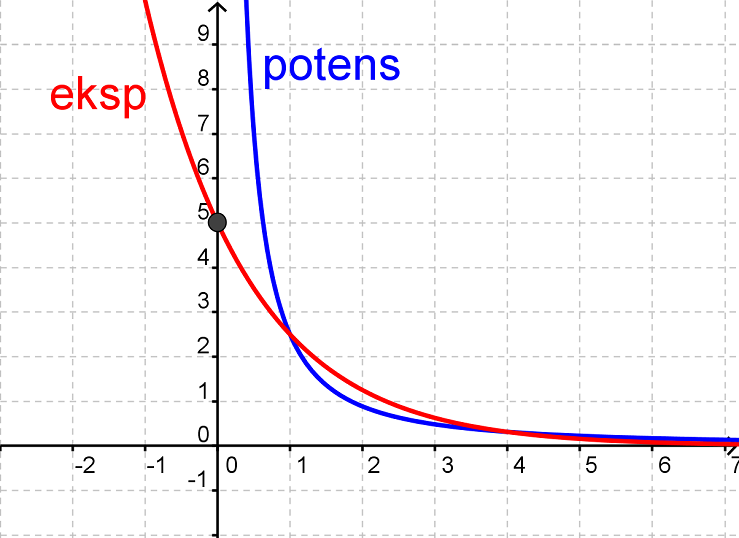
Man kan også komme til at forveksle grafen for en potensfunktion med a mindre end 0 med aftagende eksponentialfunktioner.

Her skal vi igen huske, at en aftagende eksponentialfunktion skærer y-aksen i punktet (0, b), mens en potensfunktion med a mindre end 0 aldrig skærer y-aksen.

Hvis man har nogle punkter og vil finde ud af, om de tilhører en eksponentiel eller potensvækst, kan man tegne dem ind i forskellige koordinatsystemer.

En potensfunktion vil danne en ret linje i et dobbeltlogaritmisk koordinatsystem, mens en eksponentialfunktion vil danne en ret linje i et enkeltlogaritmisk (semilogaritmisk) koordinatsystem.

Find x og y

I en potensfunktion er y en funktion af x. Hvis vi kender x, kan vi altså sætte det ind på højre side og så finde ud af, hvad det tilhørende y er.

Hvis vi derimod kender y og gerne vil bestemme x, skal vi først have isoleret x i udtrykket.

$$y=b\cdot x^a$$

$$\frac{y}{b}=x^a$$

$$\sqrt[a]{\frac{y}{b}}=x$$

Vi kan altså finde x ved formlen

$$x=\sqrt[a]{\frac{y}{b}}$$

Lad os tage et eksempel.

Hvis

$$y=4x^3$$

og vi får at vide, at x=2. Så kan vi beregne y ved at indsætte 2 på x's plads.

$$y=4x^3=4\cdot2^3=4\cdot8=32$$

y er altså 32.

Hvis vi får at vide, at y=108, så kan vi beregne x.

$$x=\sqrt[a]{\frac{y}{b}}=\sqrt[3]{\frac{108}{4}}=\sqrt[3]{27}=3$$

---

Videolektion