NCC Vinkler og vægge
Entreprenørvirksomheden NCC har siden 2015 været Matematikcenters hovedsponsor. I Matematikcenter arbejder vi for at skabe begejstring og bedre forståelse for matematik og naturvidenskab blandt børn og unge. Gennem samarbejdet med NCC vil vi vise potentialet i en erhvervsrettet eller teknisk uddannelse.
Ret eller skævt?
Som tømrer skal man ofte opsætte gipsvægge. Ved opsætning af gipsvægge, så er det sjældent, at alle vinkler mellem vægge og lofter er rette. Derfor er man nødt til, at skære pladerne, således at de passer til den eksisterende konstruktion. I videoen nedenfor fortæller Daniel om, hvordan han arbejder med opsætning af gipsvægge på skæve konstruktioner.
Cosinus og sinus
Når man regner med vinkler, så er man næsten sikker på, at løbe ind i cosinus og sinus. Cosinus og sinus er tæt relaterede til Pythagoras sætning, som Daniel også gør nytte af. Du kan se mere om Pythagoras læresætning her, og du kan læse mere om cosinus, sinus og tangens her.
Når Daniel sætter gipsplader op, og kan se, at han er nødt til at skære pladen i en skæv vinkel, så benytter han faktisk både Pythagoras læresætning, cosinus, sinus og tangens i en retvinklet trekant. Han udregner ikke nødvendigvis det hele på papir, men han gør det ved et hovedregning, også selvom han ikke nødvendigvis tænker over det.
Kender man flere sidelængder og vinkler i en retvinklet trekant, altså en trekant hvor én af vinklerne er 90 grader, så kan man ret hurtigt finde ud af, hvad de resterende vinkler eller sidelængder er.
Hvis vi forestiller os, at Daniel er ved at sætte en gipsplade op, men opdager at loftet og væggen er skæve i forhold til hinanden, hvor meget skal han så skære af sin gipsplade?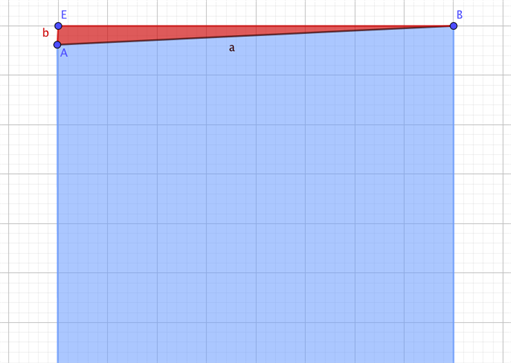
Vi ser på tegningen ovenfor. Her er det blå område en gipsplade, og det røde er det som skal skæres af gipspladen, for at den passer med loftet. Vi vil gerne vide hvor langt linjestykket EA er, altså sidelængde b. Fra tegningen ved vi, at vinkel E må være 90 grader. Vi kender desuden bredden af gipspladen, som er 0,9m, altså linjestykket EB=0,9m. Til sidst, så kender vi også vinkel B, som er 2,7 grader. Når vi kender to vinkler i en trekant, så kan vi nemt finde den sidste, da vi ved at vinkelsummen i en trekant er 180 grader. Vinkel A er derfor \( 180°-(90°+2.7°) = 87.3° \).
Vi kan nu bruge vores viden om sinus og cosinus i en retvinket trekant, til at finde længden af EA. Om sinus, cosinus og tangens i en retvinklet trekant ved vi,
$$\cos(v)=\frac{\text{hosliggende katete}}{\text{hypotenusen}}$$
$$\sin(v)=\frac{\text{modstående katete}}{\text{hypotenusen}}$$
$$\tan(v)=\frac{\text{modstående katete}}{\text{hosliggende katete}}$$
Vi husker, at hypotenusen er den længste side i den retvinklede trekant, og de to andre sider kaldes kateterne. Vi kender derfor længden af den ene katete, og så kender vi vinklerne i trekanten. Vi vil gerne finde siden EA, som er modstående katete til vinkel A. Vi bruger derfor nedernste af de tre ligninger ovenfor.
$$ \tan(A)=\frac{\text{EA}}{\text{EB}} \Rightarrow \text{EA} = \tan(A) \cdot \text{EB} $$
Vi indsætter tal og får
$$ \tan(2.7°) \cdot 0.9m = 0.042m =4.2cm $$
Daniel skal altså sørge for, at gipspladen er 4,2cm kortere i den ene siden end den anden, hvis den skal passe med loftet.
