Forskudt eksp. vækst
En anden vigtig type af differentialligninger er på formen
$$y'=b-ay$$
hvor \(a\) og \(b\) er konstanter.
Den kan eksempelvis optræde som
$$\frac{dy}{dx}=b-ay,\qquad y'+ay=b.$$
Eksempler på differentialligninger af denne type er
$$y'=8-2y,\qquad\frac{dy}{dx}+7y=37,\qquad y'-15y=17.$$
Den fuldstændige løsning til disse differentialligninger er
$$y=f(x)=\frac{b}{a}+ce^{-ax}$$
Eksempel
Hvis vi vil løse differentialligningen
$$y'=3-5y$$
er den fuldstændige løsning altså
$$y=f(x)=\frac{3}{5}+ce^{-5x}=0,\!6+ce^{-5x}$$
Havde vi fået startbetingelsen \(y(0)=14\), ville vi kunne isolere \(c\)
$$14=0,\!6+ce^{-5\cdot0} \quad \Leftrightarrow \quad 14 = 0,\!6 + c \quad \Leftrightarrow \quad c = 13,\!4$$
Den partikulære løsning ville så være
$$y=f(x)=0,\!6+13,\!4e^{-5x}$$
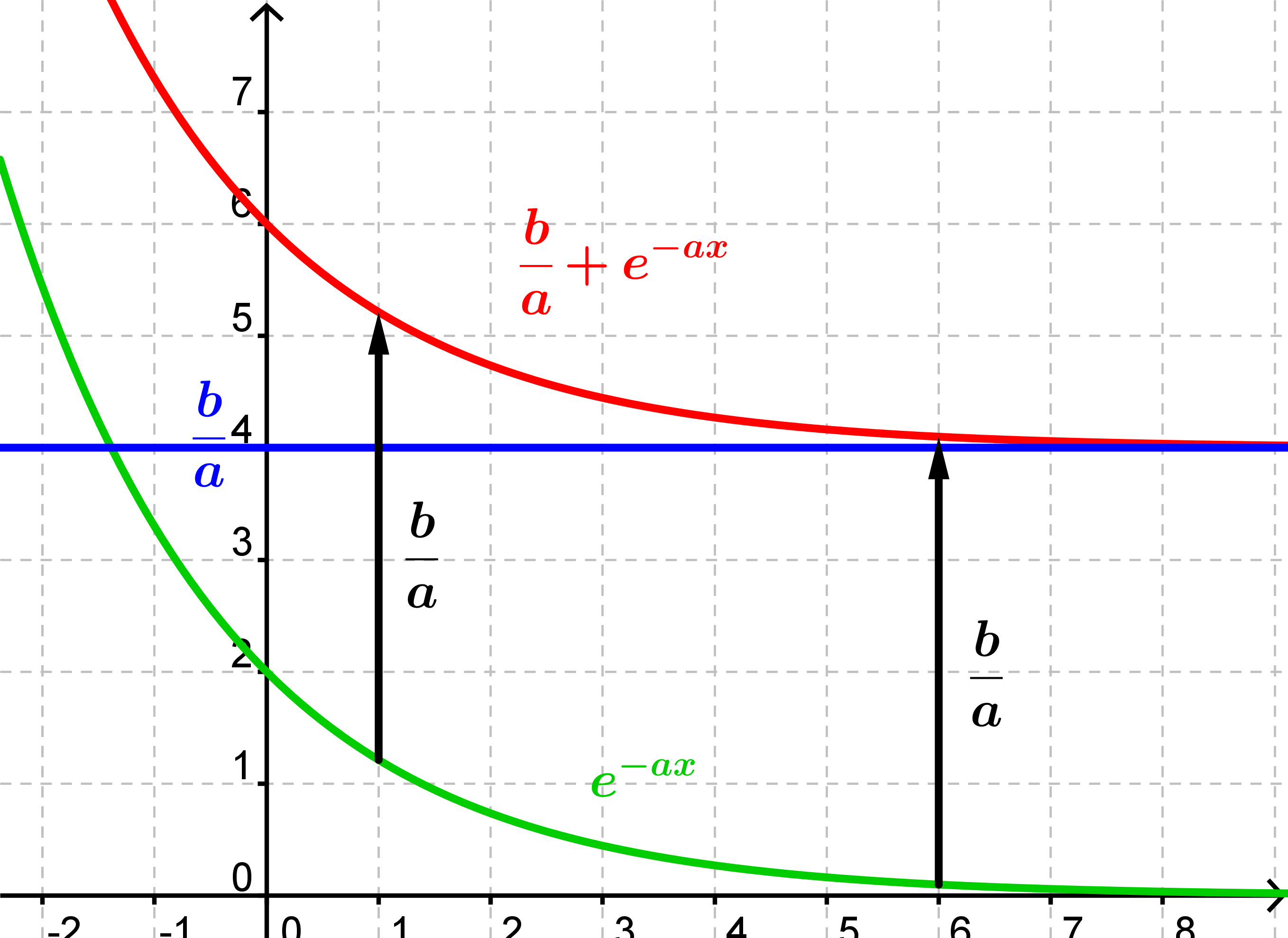
Bemærk, at løsningerne til denne type differentialligninger er forskudte eksponentialfunktioner.
Dvs. eksponentialfunktioner, hvis grafer er forskudt lodret.
Newtons afkølingslov
Differentialligninger af formen
$$y'=b-ay$$
har en nær sammenhæng med Newtons afkølingslov.
Newtons afkølingslov siger
"Hastigheden hvormed temperaturen af et legeme ændres, er proportional med forskellen mellem legemets temperatur og det omgivende rums temperatur".
Hvis vi f.eks. har en kop skoldhed te, som vi stiller i et rum med stuetemperatur, så vil den afkøles hurtigt i starten (hvor forskellen mellem teens og rummets temperatur er stor), mens den efter et stykke tid kun vil afkøles langsomt (hvor forskellen mellem teens og rummets temperatur er lille).
Lad os prøve at skrive Newtons afkølingslov om til en differentialligning.
Differentialkvotienter siger noget om funktioners hastighed. "Hastigheden hvormed temperaturen af et legeme ændres" kan vi derfor omskrive til \(y'\). Hvis vi kalder rummets temperatur for \(T\), så kan "forskellen mellem legemets temperatur og det omgivende rums temperatur" omskrives til \((T-y)\).
At to ting er proportionale betyder, at der findes en konstant, \(a\), så den ene er lig med \(a\) ganget med den anden (dvs. den ene er \(a\) gange større end den anden).
Nu siger vores differentialligning
$$y'=a(T-y)$$
Hvis vi ganger parentesen ud, får vi
$$y'=aT-ay$$
Det minder meget om vores differentialligning for forskudt eksponential vækst. Den eneste forskel er, at den konstant, vi kaldte \(b\), her hedder \(a\cdot T\).
Løsningen (dvs. den funktion, der beskriver hvordan temperaturen af legemet ændrer sig ifht. tiden) kan skrives som
$$y=f(t)=\frac{b}{a}+ce^{-a\cdot t}=\frac{a\cdot T}{a}+ce^{-a\cdot t}=T+ce^{-a\cdot t}$$
For at kunne bestemme \(c\) og \(a\) skal man have to begyndelsesbetingelser (f.eks. begyndelsestemperaturen og temperaturen efter en time)
