Niveaukurver

Du har sikkert set et kort over et landskab med mange højdeforskelle, hvor der var tegnet  kurver ind, og måske endda farveforskelle. Disse kurver er det der kaldes niveaukurver, og fortæller hvilken højde man befinder sig i. Hvis man går langs en kurve, går man hele tiden i den samme højde, og man vil derfor ofte se noget der minder om cirkler rundt om bjerge på kortet. Til at beskrive kurver, der har højdeforskelle, bruger man funktioner af to variable. Man kan finde niveaukurver til funktionerne, der fortæller langs hvilke kurver funktionen har den samme værdi.

Hvis man har en funktion af to variable, \( f(x,y) \), kan man finde niveaukurverne ved at sætte funktionen lig med en konstant, som vi kan kalde c. Vi kan således definere det, der kaldes niveaumængden:

$$ K_c = \{ (x,y) \in \mathbb{R}^2 | f(x,y)=c\} $$

Måden dette skal læses på er, at niveaumængden \( K_c \) indeholder alle de punkter \( (x,y) \), der er den del af det to-dimensionelle koordinatsystem (\( (x,y) \)-planen), hvorom det gælder at \( f(x,y)=c \). Det er altså de punkter der opfylder at funktionens værdi er c. 

Vi kan for eksempel se på funktionen \( f(x,y) = x^2+y^2-6x+4y+13 \). Hvis vi omformer den lidt, får vi noget vi kender:

$$ f(x,y) = x^2+y^2-6x+4y+13 = (x-3)^2+(y+2)^2 $$

Sættes funktionen lig konstanten c får vi cirklens ligning, for en cirkel med centrum i (3,-2) og radius \( \sqrt{c} \):

$$ (x-3)^2+(y+2)^2 = c $$

Da vi har to kvadrerede led på venstresiden, kan vores ligning ikke antage negative værdier. Den kan kun være positiv eller 0 i punktet (3,-2). Vi kan derfor opskrive vores niveaumængde i tre forskellige tilfælde:

$$K_c = \begin{cases} c<0 & K_c \in \emptyset \\ c=0 & K_c = \{(3,-2)\} \\ c>0 & K_c = \text{cirkel med centrum i (3,-2) og radius} \sqrt{c} \end{cases} $$

Her betyder Ø den tomme mængde, betydende at funktionen ikke har værdier mindre end 0 nogen steder. Det hele bliver lidt nemmere at forstå hvis man kan se det for sig. Vi kan starte med at plotte vores funktion \( f(x,y) \), for at se hvordan den egentlig ser ud:

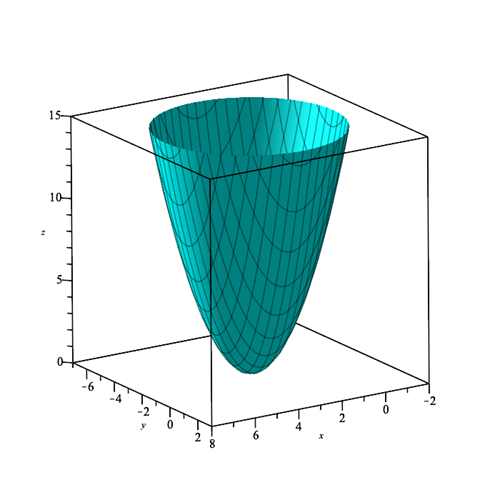
Vi kan se at funktionen har et minimum i (3,-2) med værdien 0. Derfor giver det mening, at der ikke er nogle niveaukurver tilhørende værdier mindre end 0. Vi kan også allerede nu se, at det giver mening, at funktionens niveaukurver vil være cirkler. Vi plotter nu figuren med nogle af dens niveaukurver, som farves røde:

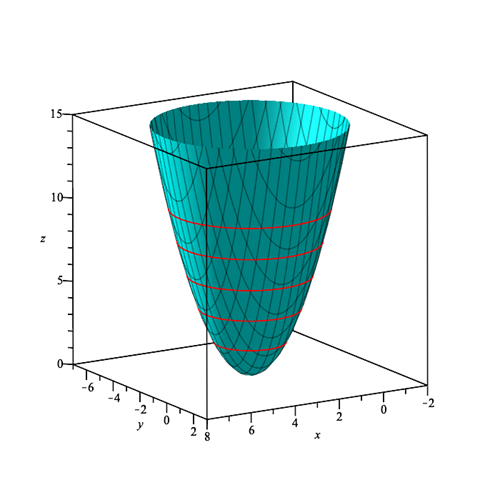
Her er der plottet kurver i højderne 2, 4, 6, 8 og 10, men vi kunne have fortsat uendeligt højt op. Som vi forudsage har kurverne form som cirkler, der bliver større og større for større c. Nogle steder kaldes det vi har plottet her for højdekurver, og niveaukurverne er så højdekurverne projiceret ned i \( (x,y) \)-planet. Det kan ses her:

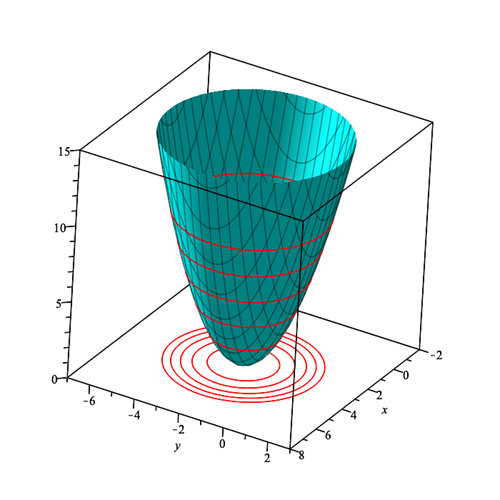
Cirklerne i planen angiver niveaukurverne, og det er en måde at afbilde noget tre-dimensionelt i det to-dimensionelle plan. Det er de kurver, man vil se på et landkort, der viser højder. Til sidst kan vi lave et konturplot, hvor de forskellige niveauer er blevet farvet, så man bedre kan visualisere højdeforskellene:

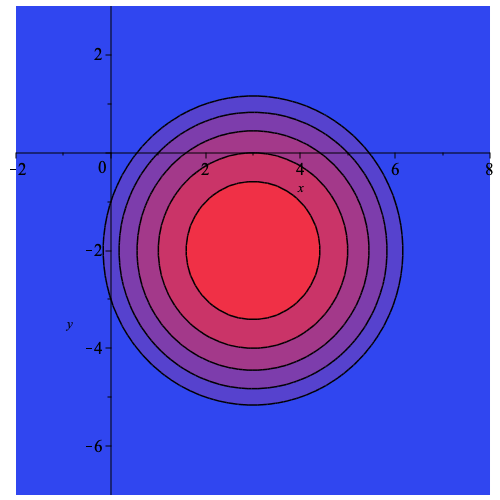
På det sidste plot er det også endnu tydeligere, at cirklerne alle har centrum i punktet (3,-2). Det kunne for eksempel være en afbildning af en bakke, som har sit toppunkt i (3,-2), og med en radius på lidt over 3.

I videoen nedenfor kan du se, hvordan alle plots i dette afsnit er lavet, og du kan selv lære at plotte niveaukurver, højdekurver og konturplots i Maple.