Tangentplan
Ligesom man kan finde tangentplanen til et bestemt punkt på en kugle, kan man også finde en tangentplan for en funktion af to variable. Det er den plan, der kun rører funktionen lige præcis i ét punkt, omkring der hvor vi finder planen - ligesom en tangentlinje til en funktion af én variabel. For en kugle kan man sige med sikkerhed, at tangentplanen kun rører et eneste punkt, fordi alle punkter på kuglen kan ses som lokale maxima. Men når det kommer til funktioner af flere variable, så kan det godt være, at planen skærer kurven igen et andet sted, ligesom med en tangentlinje.
Den generelle ligning for tangentplanen til en funktion \( f(x,y) \) i et punkt \( (x_0,y_0) \) er givet ved:
$$ z=f(x_0,y_0)+\frac{\partial f}{\partial x}(x_0,y_0)\cdot (x-x_0)+\frac{\partial f}{\partial y}(x_0,y_0)\cdot (y-y_0) $$
Hvor \( \frac{\partial f}{\partial x}(x_0,y_0) \) angiver den partielt afledede i forhold til x i punktet \( (x_0,y_0) \). Vi skal altså kende vores funktion, samt vores punkt vi ønsker at bestemme tangentplanen i. Dette punkt skal ligge på kurven for \( f(x,y) \).
Eksempel
Lad os se på funktionen \( f(x,y) = 2x^2+y^2-4x-3y+1 \), og finde tangentplanen i punktet \( (3,5,f(3,5)) \). Det første vi gør er, at bestemme funktionens værdi i (3,5):
$$ f(3,5) = 2\cdot 3^2+5^2-4\cdot 2-3\cdot 5+1=18+25-12-15+1=17 $$
Nu bestemmer vi de partielt afledede og evaluerer dem i punktet (3,5):
$$ f_x(x,y) = \frac{\partial }{\partial x} f(x,y) = 4x-4 $$
$$f_x(3,5) = 4\cdot 3-4 = 8 $$
$$ f_y(x,y) = \frac{\partial }{\partial y} f(x,y) = 2y-3 $$
$$f_y(3,5) = 2\cdot 5-3 = 7 $$
De fundne værdier kan nu indsættes i udtrykket for tangentplanens ligning:
$$ z=17+8(x-3)+7(y-5)=8x+7y-42 $$
Omformer vi lidt får vi tangentplanens ligning i punktet \( (3,5,17) \):
$$ 8x+7y-z=42 $$
Det er altså ligningen for den plan, der lige rører vores funktion i det bestemte punkt. Ud fra denne ligning kan vi aflæse en normalvektor til planen fra koefficienterne:
$$ \overrightarrow{n} =\begin{pmatrix}8\\7\\-1\end{pmatrix}$$
Nedenfor ses et plot af funktionen (den buede, grønne kurve), tangentplanen og punktet hvor de skærer hinanden:
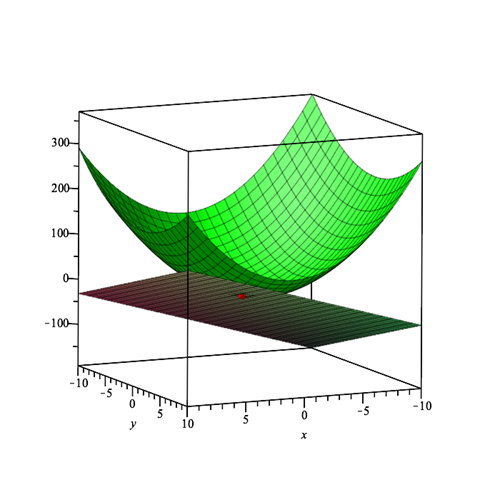
I videoen kan du se, hvordan plottet er blevet lavet, og selv lære hvordan man plotter tangentplaner:
