Vindskæve linjer
Hvis man har to linjer i rummet kan de ligge på tre forskellige måder i forhold til hinanden.
De kan
- være parallelle
- skære hinanden i et punkt
- være vindskæve
Lad os se på de tre tilfælde hver for sig.
Parallelle
Man kan undersøge, om to linjer er parallelle ved at se om deres to retningsvektorer er parallelle.
Dette kan gøres på to måder. Enten kan man undersøge om den ene er en forlængelse af den anden.
F.eks. er
$$\begin{pmatrix}3\\6\\9\end{pmatrix}$$
en forlængelse af
$$\begin{pmatrix}1\\2\\3\end{pmatrix}$$
fordi man kan skrive
$$\begin{pmatrix}3\\6\\9\end{pmatrix}=3\cdot\begin{pmatrix}1\\2\\3\end{pmatrix}$$
Den anden metode til at tjekke for parallelitet er ved at undersøge om krydsproduktet giver 0. Hvis de to retningsvektorer betegnes med r og q gælder nemlig:
$$\begin{pmatrix}r_1\\r_2\\r_3\end{pmatrix}\times\begin{pmatrix}q_1\\q_2\\q_3\end{pmatrix}=0\quad\Leftrightarrow \quad\overrightarrow{r}\parallel\overrightarrow{q}$$
Hvis linjerne er parallelle har de enten 0 skæringspunkter eller uendeligt mange skæringspunkter (dette sker, hvis de to linjer er ens)
Ét skæringspunkt
Hvis linjerne ikke er parallelle, kan man undersøge, om de skærer hinanden i ét punkt. Det gør man ved først at sætte ligningerne for de to x- og y-koordinater lig hinanden. Det vil give to ligninger med to ubekendte (de to parametre), som vi kan løse.
Når vi så har fundet løsningerne, så sætter vi parametrene ind i ligningerne for z-koordinaterne og ser, om vi får samme z-koordinat. Hvis dette er tilfældet, har vi fundet et skæringspunkt. Og hvis vi ikke får samme z-koordinat, så skærer de to linjer ikke hinanden.
Vi prøver med et eksempel. Vores linjer l og m er givet ved
$$l:\quad\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}1\\2\\4\end{pmatrix}+t\cdot\begin{pmatrix}3\\1\\2\end{pmatrix}$$
$$m:\;\, \begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}5\\1\\3\end{pmatrix}+s\cdot\begin{pmatrix}2\\4\\2\end{pmatrix}$$
Vi kan skrive ligningerne for x- og y-koordinaterne således:
$$x_l=1+3t$$
$$y_l=2+1\cdot t$$
$$x_m=5+2s$$
$$y_m=1+4s$$
Vi sætter x-værdierne lig hinanden og y-værdierne lig hinanden
$$1+3t=5+2s$$
$$2+t=1+4s$$
Vi løser de to ligninger med to ubekendte og når frem til
$$s=0,7\quad\text{og}\quad t=1,8$$
Nu skal vi indsætte disse s- og t-værdier i ligningerne for z-værdierne.
$$z_l=4+2t=4+2\cdot1,8=7,6$$
$$z_m=3+2s=3+2\cdot0,7=4,4$$
Da vi får to forskellige z-værdier, betyder det, at de to linjer ikke skærer hinanden.
Vindskæve linjer
Hvis to linjer hverken er parallelle eller skærer hinanden, så kaldes de "vindskæve". På billedet herunder har vi forsøgt at afbilde to vindskæve linjer. Deres retningsvektorer er ikke parallelle, og i det punkt, hvor de har samme x- og y-værdier (de to sorte punkter), er deres z-værdier forskellige.
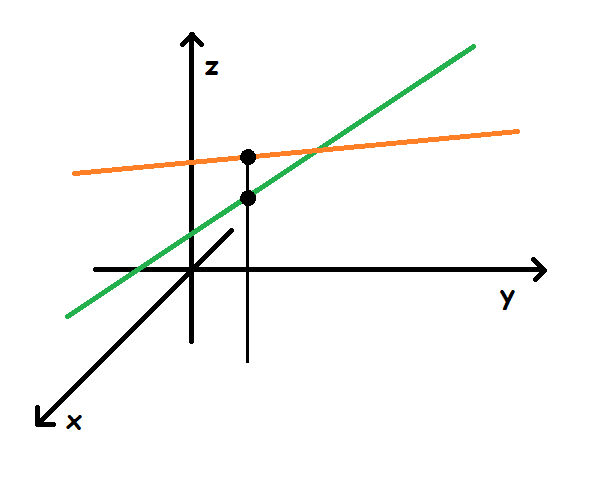
Det ligner, de skærer hinanden et sted, men det er fordi, det er svært at tegne tredimensionelt i to dimensioner. I det tilsyneladende skæringspunkt er den grønne linje "længere inde i skærmen", mens den orange er tættere på os.
Man kan forestille sig to vindskæve linjer som en bil, der kører ad en lige vej nede på jorden (den ene linje) og et fly, der flyver ligeud oppe i luften (den anden linje).
Selvom flyet krydser henover vejen, så vil bilen og flyet ikke støde sammen, da flyet befinder sig flere km over vejen.
