Optimering
En af de vigtigste anvendelser indenfor differentialregning er optimering. Det kunne f.eks. være en virksomhed, der ville maksimere sit overskud, eller en konservesfabrik, der ville minimere sit metalforbrug (overfladearealet af dåserne).
Vi vil først gennemgå et eksempel og bagefter komme med en opskrift på, hvordan man løser optimeringsproblemer.
En virksomhed producerer kasser med kvadratisk bund og uden låg. Kasserne skal kunne indeholde 1 dl (=100cm3). Bestem sidelængden af kassens bund således at kassens overfladeareal bliver mindst muligt.
Først skal vi danne os et billede over hvilken figur, det er, vi arbejder med. Kassen har kvadratisk bund. Lad os kalde sidelængderne i bundstykket for x. Lad os kalde kassens højde for h. Både x og h skal (selvfølgelig) være positive. Det vi arbejder med er altså en kasse af følgende type:
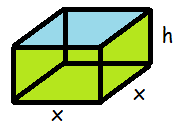
Nu skal vi danne os et overblik over, hvad vi skal optimere (i dette tilfælde minimere). Det er overfladearealet. Lad os prøve at udtrykke overfladearealet, O, ved hjælp af x og h.
Kassen har fire sider, der hver har arealet
$$A_{side}=x\cdot h$$
Derudover har den en bund, der har arealet
$$A_{bund}=x\cdot x=x^2$$
Det samlede overfladeareal er altså
$$O(x,h)=4\cdot A_{side}+A_{bund}=4xh+x^2$$
Det er altså denne funktion, vi vil finde minimum for. Imidlertid har vi et problem: den indeholder to variable (x og h), og vi kan kun finde maksima og minima for funktioner af en variabel. Heldigvis har vi fået en oplysning, der gør, at vi kan udtrykke den ene variabel med den anden. Vi har nemlig fået at vide, at kassens volumen skal være 100 cm3.
$$V=x\cdot x\cdot h=100$$
$$x^2h=100$$
$$h=\frac{100}{x^2}$$
Man skal være opmærksom på, om man er kommet til at dividere med 0 (man må aldrig dividere med 0). Men da x er en sidelængde, er den altid positiv, og derfor er x2 aldrig 0. Derfor har vi ikke foretaget os noget forbudt.
Dette udtryk for kan vi nu sætte ind på h's plads i udtrykket for overfladearealet.
$$O(x)=4x\cdot{\color{Red} {\frac{100}{x^2}}}+x^2=\frac{400}{x}+x^2,\qquad x>0$$
Nu er forarbejdet gjort. Vores funktion O(x) har kun en variabel, og vi er parat til at optimere den. Metoden er faktisk identisk med at finde dens monotoniforhold.
Først differentierer vi O(x).
$$O'(x)=400\cdot\frac{-1}{x^2}+2x^{2-1}=\frac{-400}{x^2}+2x$$
Nu sætter vi O'(x) lig med 0 for at finde de steder, hvor tangenthældningen er 0 (dvs. tangenten er vandret, dvs maksimum, minimum eller vendetangent).
$$O'(x)=0$$
$$\frac{-400}{x^2}+2x=0$$
$$2x=\frac{400}{x^2}$$
$$2x^3=400$$
$$x^3=200$$
$$x=\sqrt[3]{200}\approx5,85cm$$
Det eneste sted, hvor tangenten er vandret er altså når x≈5,85 cm. Vi mangler stadig at undersøge, om dette punkt er et minimum. Dette gør vi ved at undersøge om O' er positiv eller negativ på hver side af 5,85. Vi starter med at undersøge fortegnet på O', når x er mindre end 5,85 (men stadig større end 0). Vi vælger et tilfældigt tal i intervallet. Lad os for bekvemmeligheds skyld vælge 1.
$$O'(1)=\frac{-400}{1^2}+2\cdot1=-400+2=-398<0$$
Derefter undersøger vi fortegnet for O', når x er større end 5,85. Vi vælger at se på tallet 20.
$$O'(20)=\frac{-400}{20^2}+2\cdot20=\frac{-400}{400}+40=-1+40=39>0$$
Nu kan vi tegne en monotonilinje.
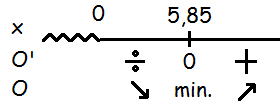
Hermed kan vi se, at 5,85 er et minimum for overfladearealet.7
Vi kan tilmeld regne ud hvor stort overfladearealet bliver i dette punkt simpelthen ved at sætte 5,85 ind på x's plads i udtrykket for overfladearealet.
$$O_{min}=O(5,85)=\frac{400}{5,85}+5,85^2\approx102,60cm^2$$
Herunder er tegnet en graf, der viser hvor stort overfladearealet bliver ved værdier af x.
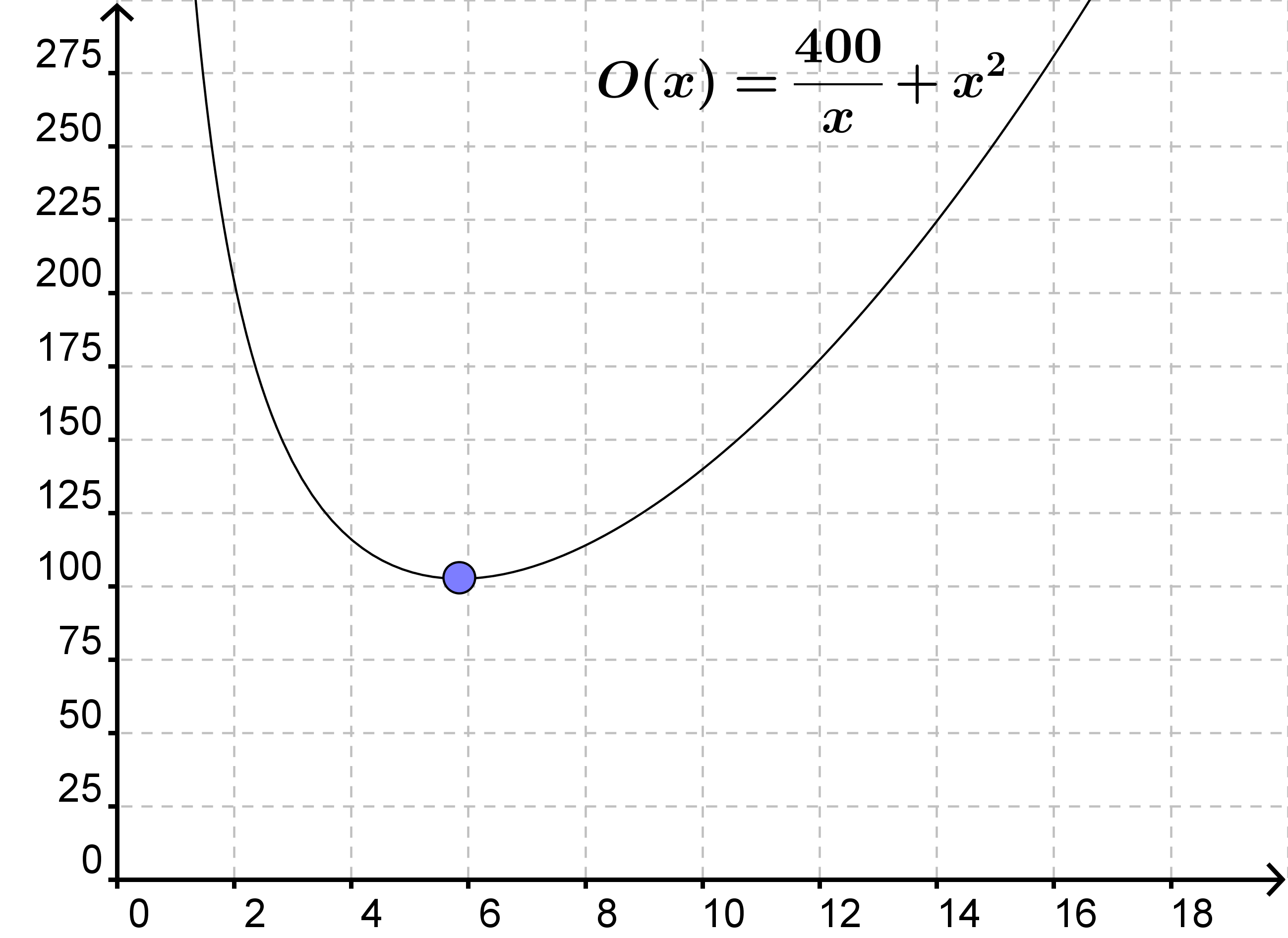
Opskrift
Her følger en opskrift på hvordan du løser optimeringsproblemer
- Opskriv den funktion, du skal optimere
- Opskriv den bibetingelse, du er blevet givet.
- Isoler den ene variabel i bibetingelsen
- Indsæt udtrykket for denne variabel i den funktion, du skal optimere.
- Nu står du tilbage med en funktion af en variabel.
- Differentier funktionen
- Løs ligningen f '(x)=0
- Bestem fortegnene for f ' mellem løsningerne
- Tegn monotonilinjen
