Projektion af vektor på vektor
Givet to egentlige vektorer kan man projicere den ene ned på den anden. Hvis man har tegnet de to vektorer fra samme begyndelsespunkt, svarer det til at gå vinkelret fra spidsen af den ene ned på den anden vektor. Vektoren fra begyndelsespunktet og hen til det punkt, man rammer, er projektionsvektoren.
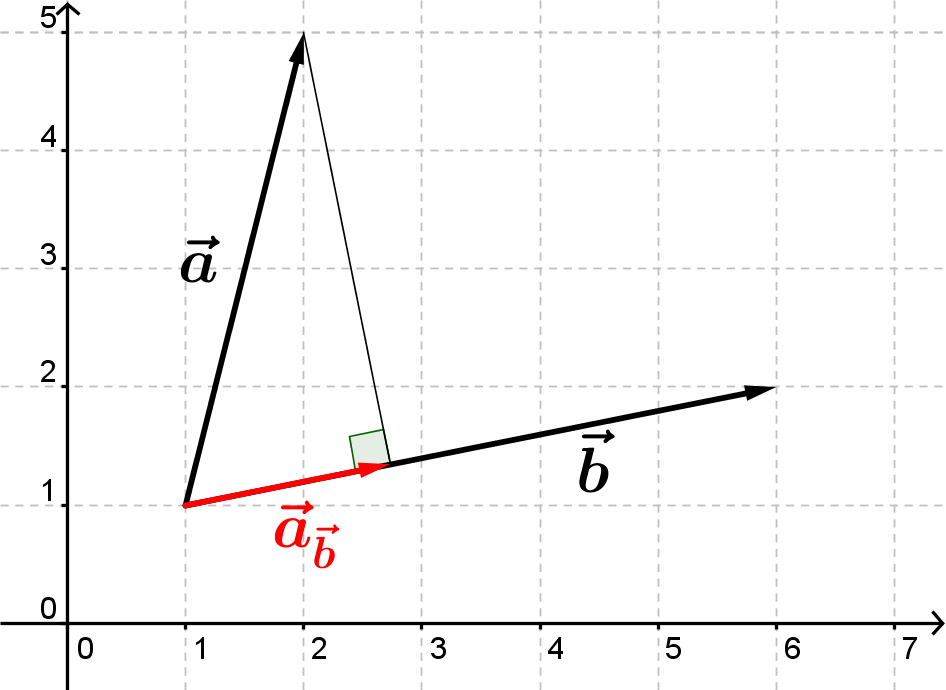
Projektionsvektoren vil selvfølgelig være parallel med den vektor, man projicerer ned på.
Der findes en formel til at beregne projektionsvektorens koordinater
$$\vec{a}_{\vec{b}}=\frac{\vec{a}\cdot\vec{b}}{|\vec{b}|^2}\cdot\vec{b}$$
Man skal holde tungen lige i munden med, hvad der er hvad. I tælleren har vi et skalarprodukt. Prikken er altså en prik. Skalarproduktet er et tal og nævneren, der består af en længde, er også et tal. Dermed giver hele brøken et tal. Højresiden skal altså læses som et tal ganget med vektor b. Den sidste prik er altså et gangetegn og ikke en prik.
Lad os udregne koordinaterne for billedeksemplet ovenfor.
$$\vec{a}=\begin{pmatrix}1\\4\end{pmatrix}\text{ og }\vec{b}=\begin{pmatrix}5\\1\end{pmatrix}$$
Vi sætter ind i formlen
$$\begin{align}
\vec{a}_{\vec{b}} &= \frac{\begin{pmatrix} 1 \\ 4 \end{pmatrix} \cdot \begin{pmatrix} 5 \\ 1 \end{pmatrix}}{ \left| \begin{pmatrix} 5 \\ 1 \end{pmatrix} \right|^2} \cdot \begin{pmatrix} 5 \\ 1 \end{pmatrix} = \frac{1 \cdot 5 + 4 \cdot 1}{\left(\sqrt{ 5^2 + 1^2 }\right)^2} \cdot \begin{pmatrix} 5 \\ 1 \end{pmatrix} \\
&=\frac{9}{26} \cdot \begin{pmatrix} 5 \\ 1 \end{pmatrix} = \begin{pmatrix} \frac{45}{26} \\ \frac{9}{26} \end{pmatrix} \approx \begin{pmatrix}1,73 \\ 0,35\end{pmatrix} \end{align}$$
På tegningen ovenfor var projektionen en forkortelse af vektor b. Men sådan behøver det ikke at være. Projektionensvektoren kan godt være længere end den vektor, der projiceres på, og den kan endda være modsatrettet. Se f.eks. disse to eksempler
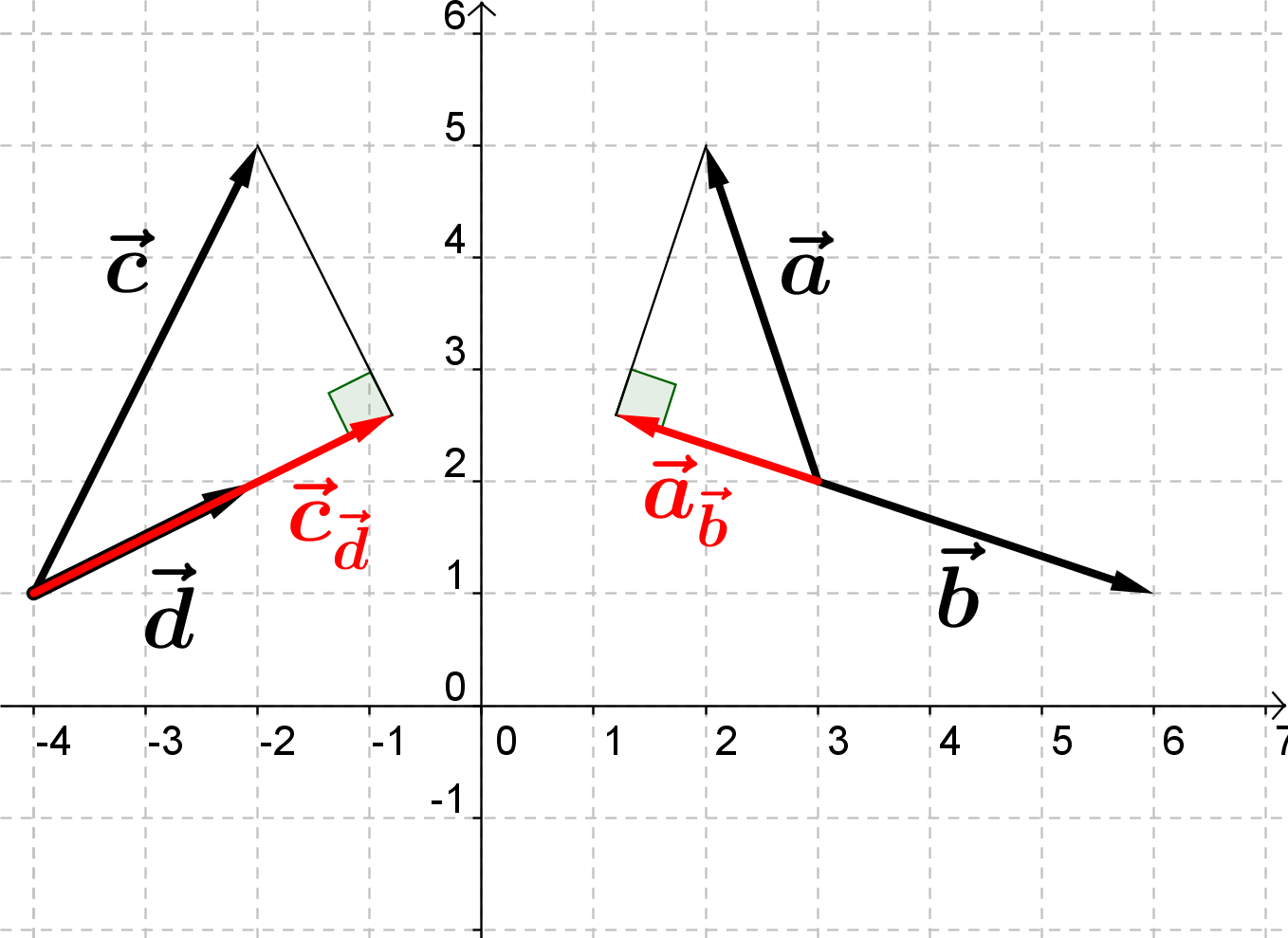
Længde af projektion
Projektionen af en vektor ned på en anden vektor har selvfølgelig også en længde. Formlen for længden af projektionen af en vektor er
$$ \left|\vec{a}_{\vec{b}}\right| = \frac{|\vec{a} \cdot \vec{b}|}{|\vec{b}|} \ , $$
som siger at længden af projektionen af vektor \(\vec{a}\) på vektor \(\vec{b}\) er givet som den absolutte værdi (også kaldet den numeriske værdi) af skalarproduktet mellem de to vektorer delt med længden af vektor \(\vec{b}\).
Lad os se på hvorfor formlen ser sådan ud. Hvis vi tager udgangspunkt i formlen for projektionen af en vektor på en vektor
$$\vec{a}_{\vec{b}}=\frac{\vec{a}\cdot\vec{b}}{|\vec{b}|^2}\cdot\vec{b}$$
så kan vi tage længden af dette udtryk og få
$$\left|\vec{a}_{\vec{b}}\right|=\left|\frac{\vec{a}\cdot\vec{b}}{|\vec{b}|^2}\cdot\vec{b}\right| \ .$$
Da \(\vec{a} \cdot \vec{b}\) er et tal kan vi betegne det med \(k\). Dermed har vi
$$ \left| k \cdot \vec{b} \right| $$
stående i tælleren. Dette er dog det samme som
$$ \left| k \right | \cdot \left| \vec{b} \right| \ .$$
Sætter vi dette ind i formlen ovenfor får vi
$$\left|\vec{a}_{\vec{b}}\right|=\frac{\left|\vec{a}\cdot\vec{b}\right|}{|\vec{b}|^2}\cdot\left|\vec{b}\right| = \frac{\left|\vec{a}\cdot\vec{b}\right|}{|\vec{b}|}$$
da
$$ \left| \vec{b} \right|^2 = \left| \vec{b} \right| \cdot \left| \vec{b} \right| . $$
Eksempel
Lad os regne længden af projektionen beregnet ovenfor. Vi har allerede regnet prikproduktet mellem de to vektorer til
$$ \vec{a} \cdot \vec{b} = 9 \, $$
så at tage den numeriske værdi ændrer ikke noget, da tallet er positivt. Længden af vektor \(\vec{b}\) er desuden
$$ \left|\vec{b}\right| = \sqrt{5^2 + 1^2} = \sqrt{26} \ .$$
Sætter vi ind i formlen for længden af projektionen finder vi at længden af projektionen af vektor \(\vec{a}\) på \(\vec{b}\) er
$$ \left|\vec{a}_{\vec{b}}\right| = \frac{9}{\sqrt{26}} \approx 1,\!77 \ . $$
