Tre ligninger med tre ubekendte
Hvis man uden problemer kan løse to ligninger med to ubekendte, kan man også løse tre ligninger med tre ubekendte. Der er flere metoder til at løse sådan et problem på: Den ene er vha. et CAS-værktøj som fx Maple eller TI-Nspire. Den anden metode er ved håndkraft, og den skal vi se lidt nærmere på her.
Lad os starte med at se på disse ligninger:
$$ (I): \qquad x+y+z=5 $$
$$ (II): \qquad 2x-y+z=9 $$
$$ (III): \qquad x-2y+3z=16. $$
Disse ligninger kan kombineres på følgende måder: (I) og (II), (I) og (III) og (II) og (III). Vi starter med at vælge to af kombinationerne, og det er faktisk ligegyldigt, hvilke man vælger. Vi vælger (I) og (II) samt (I) og (III). Vi skal også vælge, hvilken variabel vi vil eliminere, dvs. hvilken variabel vi vil beskrive vha. de andre variable. Igen er det ligegyldigt, hvilken variabel, vi vælger her. Vi vælger varablen \(z\) og isolerer altså \(z\) i ligningerne (I) og (II).
$$ (I): \qquad x+y+z=5 \Leftrightarrow z=5-x-y $$
$$ (II): \qquad 2x-y+z=9 \Leftrightarrow z=9-2x+y $$
I den første ligning har vi trukket \(x\) og \(y\) fra på begge sider af lighedstegnet, og i den anden ligning har vi trukket \(2x\) fra og lagt \(y\) til på begge sider af lighedstegnet. Nu har vi to forskellige udtryk, der beskriver variablen \(z\). Vi definerer nu en 4. ligning ved at sætte udtrykkene for \(z\) lig med hinanden, og derefter isolerer vi en af de tilbageværende variable, enten \(x\) eller \(y\). Her vælger vi at isolere \(x\).
$$ (IV): \qquad 5-x-y=9-2x+y $$
$$ \qquad \qquad \Leftrightarrow 2x-x=9+y+y-5 $$
$$ \qquad \qquad \Leftrightarrow x=2y+4 $$
Her har vi lagt \(2x\) og \(y\) til på begge sider og trukket 5 fra på begge sider, og den 4. ligning er altså: \(x = 2y + 4\).
Nu kigger vi på den anden kombination, nemlig ligningerne (I) og (III). Her skal vi først isolere den samme variabel, som vi startede med at isolere i ligningerne (I) og (II), dvs. variablen \(z\).
$$ (I): \qquad x+y+z=5 \Leftrightarrow z=5-x-y $$
$$ (III): \qquad x-2y+3z=16 $$
$$ \qquad \qquad \Leftrightarrow 3z=16-x+2y $$
$$ \qquad \qquad \Leftrightarrow z=\frac{16}{3} - \frac{1}{3}x + \frac{2}{3}y $$
I (III) har vi først trukket \(x\) fra og lagt \(2y\) til på begge sider, hvorefter vi har divideret med 3 for at isolere \(z\). Igen har vi nu to udtryk, der beskriver \(z\) ud fra \(x\) og \(y\). Nu sætter vi disse to udtryk lig med hinanden og isolerer \(x\):
$$ (V): \qquad \frac{16}{3} - \frac{1}{3} x + \frac{2}{3} y = 5-x-y $$
$$ \qquad \qquad \Leftrightarrow 16-x-2y=15-3x-3y $$
$$ \qquad \qquad \Leftrightarrow 3x-x = 15-3y-2y-16 $$
$$ \qquad \qquad \Leftrightarrow 2x=-5y-1 $$
$$ \qquad \qquad \Leftrightarrow x = -\frac{5}{2}y-\frac{1}{2}. $$
Først har vi ganget med 3 på begge sider for at fjerne nævneren på venstre side, og derefter har vi isoleret \(x\) ved at lægge \(3x\) til på begge sider og trække \(2y\) og 16 fra på begge sider. Til sidst har vi divideret med 2 på begge sider, og den 5. ligning er altså: \(x = -\frac{5}{2}y - \frac{1}{2}\).
Vi har nu to nye ligninger (IV) og (V), som begge udtrykker variablen \(x\). Nu sætter vi ligningerne (IV) og (V) lig med hinanden. På den måde får vi én ligning med én ubekendt:
$$ 2y+4=-\frac{5}{2}y-\frac{1}{2} $$
$$ \Leftrightarrow 4y+8=-5y-1 $$
$$ \Leftrightarrow 9y=-9 $$
$$ \Leftrightarrow y=-1 $$
Først har vi ganget med 2 på begge sider for at fjerne nævneren på højre side, og derefter har vi isoleret \(y\) ved at lægge \(5y\) til på begge sider og trække 8 fra på begge sider.
Nu har vi bestemt værdien for \(y\), nemlig -1, og vi bestemmer værdien for \(x\) ved at indsætte værdien for \(y\) i et af de forrige udtryk for \(x\) og får:
$$x = 2 \cdot (-1) + 4 = -2 + 4 = 2$$
Nu har vi bestemt værdien for \(x\), nemlig 2, og vi bestemmer værdien for \(z\) ved at indsætte værdierne for \(x\) og \(y\) i et af de forrige udtryk for \(z\) og får:
$$ z = 5 - 2 - (-1) = 5 - 2 + 1 = 4 $$
Løsningen er hermed: \( \qquad x=2, \qquad y=-1, \qquad z=4 \)
Vi kontrollerer, om løsningen er rigtig, ved at indsætte de fundne værdier i de tre oprindelige ligninger og tjekke, om de giver hhv. 5, 9 og 16:
$$ (I): \qquad 2+(-1)+4=2-1+4=5 $$
$$ (II): \qquad 2 \cdot 2 - (-1) +4=4+1+4=9 $$
$$ (III): \qquad 2-2 \cdot (-1)+3 \cdot 4 = 2+2+12 = 16 $$
Det passer med de fundne værdier. Denne metode kaldes for elimineringsmetoden, fordi man eliminerer de variable én efter én, indtil man kun har én variabel tilbage, som man kan bestemme værdien af. Herefter bruger man den kendte værdi til at bestemme værdien af de andre variable.
Der er også en anden metode, vi kan bruge inden for eliminering. Her eliminerer vi de variable én efter én ved enten at trække hele ligninger fra hinanden og/eller lægge hele ligninger sammen, indtil vi står tilbage med én ligning med én ubekendt.
Vi bruger de samme ligninger som i eksemplet før til at vise denne metode, og vi bruger igen de tre kombinationer, vi har beskrevet: (I) og (II), (I) og (III) samt (II) og (III). Vi husker, at det er tilladt at gange ligninger med en konstant på begge sider, så længe vi ikke ganger med 0.
Ligningerne er:
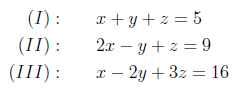
Vi starter med at lægge (I) og (II) sammen:
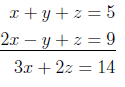
Vi ser, at variablen \(y\) er blevet elimineret. Vi kalder den nye ligning for \(IV: \, 3x + 2z = 14\).
Nu ser vi på (I) og (III). Vi skal igen have elimineret variablen \(y\), og det kan vi gøre ved at gange ligning (I) med 2 og derefter lægge den sammen med ligning (III):
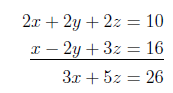
Vi kalder den nye ligning for: \(V: \quad 3x + 5z = 26\).
Nu bruger vi ligningerne (IV) og (V) til at eliminere variablen \(x\) ved at udregne (V) - (IV), og vi får:
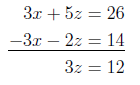
Vi har nu kun én variabel, \(z\), tilbage, og vi bestemmer værdien for denne ved at dividere med 3 på begge sider, dvs. \(z = 4\).
Vi bestemmer værdien for \(x\) ved at indsætte værdien for \(z\) enten i ligning (IV) eller i ligning (V) og får:
$$ \begin{align} 3x + 5 \cdot 4 &= 26 \\ 3x + 20 &= 26 \\ 3x &= 6 \\ x &= 2 \end{align} $$
Nu har vi bestemt værdierne for \(x\) og \(z\), og vi bestemmer værdien for \(y\) ved at indsætte værdierne for hhv. \(x\) og \(z\) i en af de oprindelige ligninger, og vi får:
$$ \begin{align} 2 + y + 4 &= 5 \\ y + 6 &= 5 \\ y &= -1 \end{align} $$
Hermed er løsningen (heldigvis) den samme som ved den første metode; \(x=2, \qquad y=-1, \qquad z=4 \).
Husk at kontrollere, om løsningen er rigtig, ved at indsætte de fundne værdier i de tre oprindelige ligninger og tjekke, om venstre side er lig med højre side.
Elimineringsmetoden kan beskrives ved disse 5 trin:
| Trin |
Beskrivelse
|
| Trin 1 |
Vælg først en af kombinationerne fra ligningssytemet |
| Trin 2 |
Vælg så en anden kombination fra ligningssystemet |
| Trin 3 |
Vælg de nye ligninger med to variable fra "Trin 1" og |
| Trin 4 |
Værdien af variablen fundet i "Trin 3" indsættes i den |
| Trin 5 |
Den sidste værdi findes ved at indsætte de fundne |
