Svingninger og periodiske funktioner
En periodisk funktion er en funktion, der opfylder, at \( f(x+T) = f(x) \) for et tal \( T \). Tallet \( T \) kaldes ofte perioden eller svingningstiden. \( T \) fortæller, hvor langt du skal gå ud ad \( x \)-aksen, før du får samme funktionsværdi, som du havde i det punkt, du startede i. Typiske eksempler på periodiske funktioner er vores trigonometriske funktioner, cosinus, sinus og tangens. Perioden for \( \cos(x) \) og \( \sin(x) \) er \( 2 \pi \), da det svarer til, at vi er gået en hel gang rundt i enhedscirklen, og vi dermed står i det punkt, vi startede i. Se figuren nedenfor, den røde graf er \( \cos(x) \), mens den blå graf er \( \sin(x) \).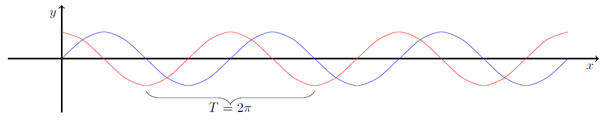
En periodisk funktion kan være på formen
$$ f(t) = A \sin( \omega t + \varphi) + k$$
Før vi begynder at undersøge betydningen af alle konstanterne, \( A , \omega , \varphi , k \), lad os lige give navnene til konstanterne
- \( A \) kaldes amplituden.
- \( \omega \) (det græske bogstav, omega), kaldes vinkelfrekvensen.
- \( \varphi \) (det græske bogstav, phi, udtales fi), kaldes faseforskydningen.
- \( k \) har ikke noget særligt navn. Den kan kaldes en forskydningskonstant - hvilket ikke bør blandes sammen med faseforskydningen.
Lad os nu undersøge en konstant af gangen.
Amplituden
Lad os betragte funktionen
$$ f(t) = A \sin(t). $$
Da \( \sin(t) \) svinger mellem \( -1 \) og \( 1 \), vil \( A \sin(t) \) svinge mellem \( -A \) og \( A \), idet vi bare har ganget alle værdierne, som \( \sin(t) \) spytter ud med \( A \). Ved at variere \( A \) kan vi således ændre funktionens udsving. I figuren herunder har vi skitseret \( f \) med forskellige værdier for \( A \):
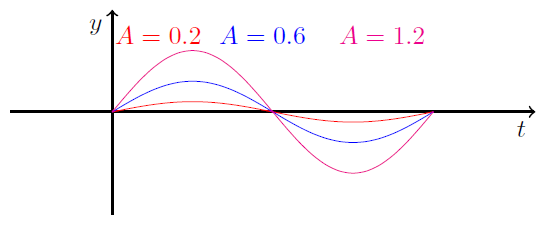
Vinkelfrekvensen
Lad os betragte funktionen
$$ f(t) = \sin(\omega t). $$
Hvis \( \omega \) er stor, vil \( \omega t \) være større end \( t \). For eksempel, hvis \( \omega = 2 \) og \( t \) løber fra \( 0 \) til \( 2 \pi \), vil \( \omega t \) løbe fra \( 0 \) til \( 4 \pi \). Det vil sige, at \( \sin ( \omega t ) \) vil nå at løbe 2 perioder igennem på samme tid som \( \sin(t) \) når 1 periode igennem, altså er frekvensen for \( \sin (\omega t ) \) dobbelt så stor som for \( \sin (t) \).
Omvendt gælder det, hvis \( \omega \) er lille, vil \( \omega t \) være mindre end \( t \). Eksempelvis gælder det, at hvis \( \omega = 1/2 \) og \( t \) løber fra \( 0 \) til \( 2 \pi \), vil \( \omega t \) løbe fra \( 0 \) til \( \pi \). Det vil sige, \( \sin ( \omega t ) \) vil nå at løbe en halv periode igennem på samme tid som \( \sin(t) \) når 1 periode igennem, altså er frekvensen for \( \sin ( \omega t ) \) halvt så stor som for \( \sin (t) \). I figuren nedenfor er der skitseret 3 grafer med forskellige værdier for \( \omega \).
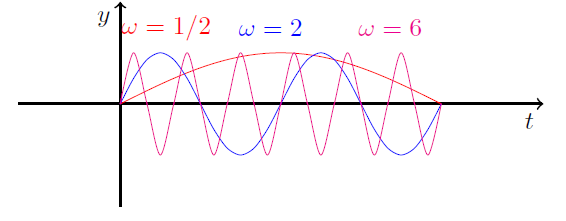
Faseforskydningen
Lad os betragte funktionen
$$ f(t) = \sin(t + \varphi). $$
Igen gælder det, at hvis \( t \) løber fra \( 0 \) til \( 2 \pi \), vil \( \sin (t + \varphi ) \) løbe fra \( 0 + \varphi = \varphi \) til \( 2 \pi + \varphi \). Det vil sige, at vi får forskudt hele svingningen med tiden \( \varphi \). Nedenunder er et par eksempler på forskellige valg af \( \varphi \).
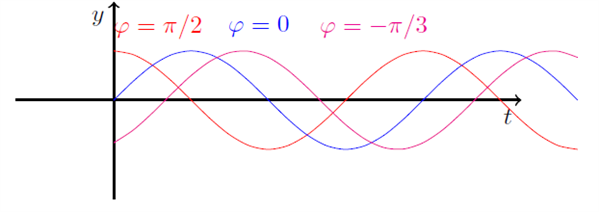
Bemærk, at hvis der er positiv faseforskydning, rykkes grafen mod venstre, mens en negativ faseforskydning giver en forskydning af grafen mod højre.
Konstanten \( k \)
Hvis du har et udtryk på formen
$$ f(t) = \sin(t)+k,$$
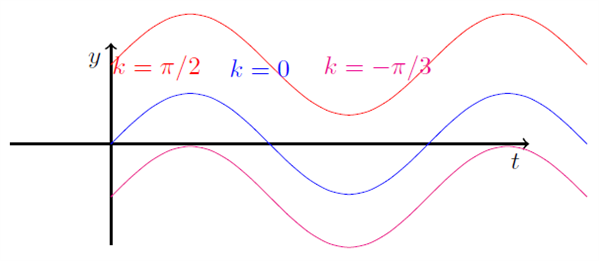
bliver der lagt \( k \) til alle funktionsværdierne for \( \sin (t) \). I modsætning til faseforskydningen, vil dette føre til en forskydningen langs \( y \)-aksen. Se figuren nedenfor
Svingningstid, frekvens og vinkelfrekvens
Alle disse 3 ord er forskellige udtryk for, hvor hurtigt en svingning oscillerer (svinger). Lad os prøve at italesætte forskellene.
Vi betragter en svingning på formen
$$ f(t) = A \sin( \omega t + \varphi) + k. $$
Svingningstid er den tid det tager svingningen at gennemløbe en periode. Det vil sige det, vi kaldte \( T \) ovenfor. Først bemærker vi, at amplituden, \( A \), faseforskydningen \( \varphi \) og \( k \) ikke har nogen indflydelse på, hvor hurtigt grafen svinger. Svingningstiden skal opfylde at
$$ \sin( \omega(t+T) = \sin (\omega t) .$$
Da \( \sin(t) \) har periode \( 2 \pi \), skal forskellen på \( \omega(t+T) \) og \( \omega t \) være en periode for \( \sin(t) \), altså \( 2 \pi \). Det vil sige, at vi kan finde \( T \) ved at løse ligningen
$$ \omega (t+T) - \omega(t) = 2 \pi ,$$
hvilket betyder, at \( \omega T = 2 \pi \), så
$$ T = \frac{2 \pi}{\omega}.$$
Vinkelfrekvensen er antallet af perioder en svingning gennemløber på et omløb i enhedscirklen, det vil sige antallet af perioder på et tidsinterval af længde \( 2 \pi \) sekunder (motivation kan findes i figuren i afsnittet om vinkelfrekvensens betydning).
Frekvensen er antallet af perioder en svingning gennemløber på et sekund. Hvis husker på, at vinkelfrekvensen var antallet af svingninger på et \( 2 \pi \) sekunders interval, vil antallet af svingninger på et sekund være vinkelfrekvensen divideret med \( 2 \pi \). Det vil sige, at
$$ f = \frac{ \omega }{ 2 \pi }.$$
Hvis vi husker, at \( T = \frac{ 2 \pi}{ \omega} \), genkender vi frekvensen som
$$ f = \frac{1}{T}.$$
