Ligevægt (lige store modsatrettede vektorer)

Ligevægt med 2 vektorer:                                                      

Vi kan kigge på to vektorer, som er lige store og modsatrettede. Vi kan se på et eksempel, hvor $$\overrightarrow{a}=\begin{pmatrix}-2\\1\end{pmatrix} \, \, \, og \, \, \, \, \,  \overrightarrow{b}=\begin{pmatrix}2\\-1\end{pmatrix}$$

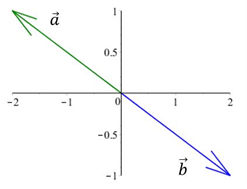
Hvis vi addere disse to vektorer     $$\overrightarrow{a}+\overrightarrow{b}=\begin{pmatrix}a_1+b_1\\a_2+b_2\end{pmatrix}=\begin{pmatrix}-2+2\\1-1\end{pmatrix}=\begin{pmatrix}0\\0\end{pmatrix}\\$$   får vi, at summen af de vektorer er lig nul-vektoren. Generelt kan vi sige, at for lige store modsatrettede vektorer gælder, at:  

$$\overrightarrow{a}+\overrightarrow{b}=\begin{pmatrix}0\\0\end{pmatrix}\\$$ Vi siger, at vi har ligevægt, når vi har lige store modsatrettede vektorer. 

Ligevægt for et vilkårlig antal vektorer:                                                              Vi har her kun betragtet et tilfælde med 2 vektorer, men dette gælder selvfølgelig også for et vilkårligt antal vektorer. Her er det illustreret med 4 vektorer: $$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}=\begin{pmatrix}0\\0\end{pmatrix}\\$$

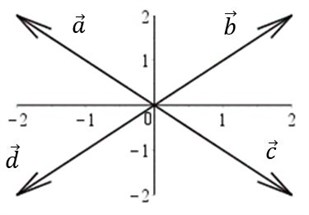
Visuel måde at se ligevægt:                                                                                     En visuel måde at vide, om et system er i ligevægt, er ved at tjekke om vektorerne danner en lukket struktur. Dvs. vi kan nu kigge på 2 eksempler og se visuelt om systemet er i ligevægt:

               

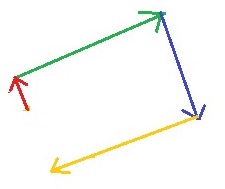
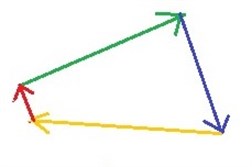
 Ikke i ligevægt!                                                  I ligevægt!

Eks. 1 - finde en vektor for at skabe ligevægt:                                                   

Vi har vektorerne  $$\overrightarrow{a}=\begin{pmatrix}3\\3\end{pmatrix} \, , \, \, \overrightarrow{b}=\begin{pmatrix}-2\\-6\end{pmatrix} \, \, {og}  \, \, \, \,  \overrightarrow{c}=\begin{pmatrix}-2\\5\end{pmatrix}$$

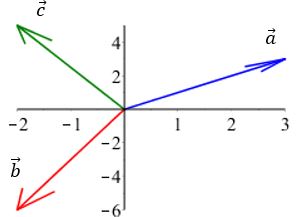
Hvilken vektor d vil skabe ligevægt i systemet?$$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}=\begin{pmatrix}0\\0\end{pmatrix}$$ $$\implies\begin{pmatrix}3\\3\end{pmatrix}+\begin{pmatrix}-2\\-6\end{pmatrix}+\begin{pmatrix}-2\\5\end{pmatrix}+\overrightarrow{d}=\begin{pmatrix}0\\0\end{pmatrix}$$ $$                       \implies\overrightarrow{d}=\begin{pmatrix}-3\\-3\end{pmatrix}+\begin{pmatrix}2\\6\end{pmatrix}+\begin{pmatrix}2\\-5\end{pmatrix}=\begin{pmatrix}-3+2+2\\-3+6-5\end{pmatrix}=\begin{pmatrix}1\\-2\end{pmatrix}$$

 Vi kan nu indtegne vektor d, som skaber ligevægt i systemet.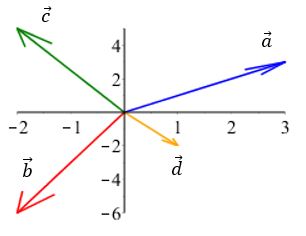

Eks. 2 - er systemet i ligevægt?                                                                          

Vi har fået givet vektorerne $$\overrightarrow{a}=\begin{pmatrix}2\\4\end{pmatrix} \, \, , \, \ \overrightarrow{b}=\begin{pmatrix}4\\-6\end{pmatrix} \, \, , \, \ \overrightarrow{c}=\begin{pmatrix}-3\\-4\end{pmatrix} \, \, \mathrm{og} \, \, \, \overrightarrow{d}=\begin{pmatrix}-5\\4\end{pmatrix}$$

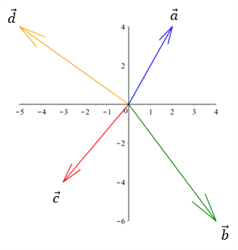 Vi kan udregne ved brug af vores formler, om der er ligevægt i systemet:  $$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}=\begin{pmatrix}2\\4\end{pmatrix}+\begin{pmatrix}4\\-6\end{pmatrix}+\begin{pmatrix}-3\\-4\end{pmatrix}+\begin{pmatrix}-5\\4\end{pmatrix}=\begin{pmatrix}-2\\-2\end{pmatrix}$$ Da det ikke giver en nulmatrice ved vi, at systemet IKKE er i ligevægt.

Eks. 3 - bringe et system i ligevægt:                                                                    

Vi hænger et maleri op i to snore på væggen i 45 graders vinkler. Tyngdekraften w har størrelsen 20 N. Vi ønsker ligevægt, så billedet hænger lige og stille, 

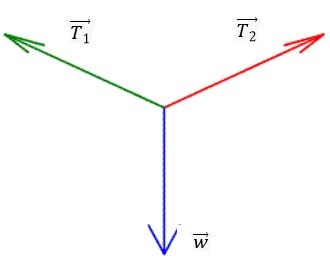
dvs. $$\overrightarrow{w}+\overrightarrow{T_1}+\overrightarrow{T_2}=\begin{pmatrix}0\\0\end{pmatrix}$$ Vi får oplyst, at tyngdekraften w har størrelsen$$\left|\overrightarrow{w}\right|=20 N=\begin{pmatrix}0\\-20\end{pmatrix}N$$ og at vinklen mellem spændingskrafterne T₁ og T₂ og tyngdekraften er 45 grader.  Spændingskrafter er de krafter, som påvirker maleriet, fordi der er en spænding i snorene, som maleriet hænger i.  Vi kan benytte viden om retvinklede trekanter for at finde de resterende krafter. 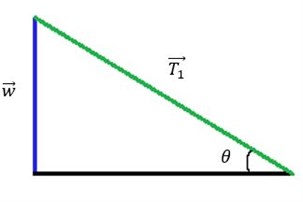                                 $$sin(\theta)=\frac{modstående}{hypotenusen}=\frac{\dfrac{\left|\overrightarrow{w}\right|}{2}}{\left|\overrightarrow{T_1}\right|}$$ $$\rightarrow\sin(45)=\frac{\dfrac{20N}{2}}{\left|\overrightarrow{T_1}\right|}$$ $$\rightarrow\left|\overrightarrow{T_1}\right|=\frac{10N}{sin(45)}=14.14N$$ Vi ved at de to spændingskrafter hiver i hver sin retning, dvs. de er modsatrettede og skal være lige store, da der ellers ikke vil være ligevægt i systemet. Derfor er $$\left|\overrightarrow{T_1}\right|=\left|\overrightarrow{T_2}\right|=14.14N$$ Vi har nu alle længderne af vektorerne, så nu skal selve vektorerne findes for de to "spændingskrafter". Y-komponenten for begge spændingskrafter er halvdelen af tyngdekraftens y-komponent, da de har samme størrelse i y-retningen, dvs. $$\overrightarrow{T_{y_1}}+\overrightarrow{T_{y_2}}+\overrightarrow{w_y}=\begin{pmatrix}0\\0\end{pmatrix}\rightarrow \overrightarrow{T_{y_1}}=\overrightarrow{T_{y_2}}=\begin{pmatrix}0\\10\end{pmatrix}$$ Nu skal x-komponenten udregnes. Vi ved at de to spændingskrafter hiver i hver deres retning, dvs. de er modsatrettede og skal være lige store, da der ellers ikke vil være ligevægt i systemet.                                                                            Vi udregner først størrelsen af de to x-komponenter: $$\left|\overrightarrow{T_x}\right|=\left|\overrightarrow{T}\right|\cdot\cos(\theta)\implies\left|\overrightarrow{T_x}\right|=14.14N\cdot\cos(45)=10N$$ Dvs. vi ved, at de skal have størrelsen 10N i hver deres retning: $$\overrightarrow{T_{x_1}}+\overrightarrow{T_{x_2}}=\begin{pmatrix}0\\0\end{pmatrix}\implies\overrightarrow{T_{x_1}}=\begin{pmatrix}10\\0\end{pmatrix}N \, \,  og \, \, \, \overrightarrow{T_{x_2}}=\begin{pmatrix}-10\\0\end{pmatrix}N$$

Dvs. vi har komponenterne for de to spændingsvektorer nu. Vi kan derfor tjekke om der er ligevægt i systemet   $$\overrightarrow{w}+\overrightarrow{T_1}+\overrightarrow{T_2}=\begin{pmatrix}0\\0\end{pmatrix}\rightarrow\begin{pmatrix}0\\-20\end{pmatrix}N+\begin{pmatrix}10\\10\end{pmatrix}N+\begin{pmatrix}-10\\10\end{pmatrix}N=\begin{pmatrix}0\\0\end{pmatrix}$$

 

Industrieksempel - Ligevægt i en bro                                      

Vi fokuserer på en bestemt del af broen, som bliver påvirket af 5 forskellige krafter, som vist på figuren. Her er størrelsen af T₁ lig T₂ og størrelsen af T₃ er lig T_4 .

      

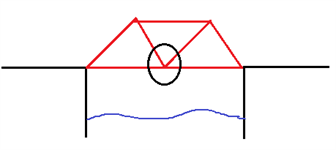
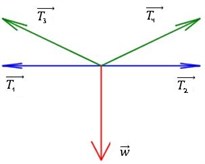
Vi får oplyst, at tyngdekraften w har størrelsen 1000N , og at de horisontale krafter T₁ og T₂ har størrelsen 200N. Desuden får vi at vide, at vinklen mellem T₁ og T₃ er 45 grader, og det samme med T₂ og T₄ .                                      

Vi skal udregne størrelserne og værdierne af krafterne, så systemet er i ligevægt, dvs. vi ønsker en situation, hvor $$\overrightarrow{w}+\overrightarrow{T_{1}}+\overrightarrow{T_{2}}+\overrightarrow{T_{3}}+\overrightarrow{T_{4}}=\begin{pmatrix}0\\0\end{pmatrix}$$

De to krafter, som kun virker i det vandrette plan, T₁ og T₂, har lige stor størrelse, så de skaber ligevægt med hinanden. $$\overrightarrow{T_{1}}+\overrightarrow{T_{2}}=\begin{pmatrix}0\\0\end{pmatrix}\implies\begin{pmatrix}200\\0\end{pmatrix}N+\begin{pmatrix}-200\\0\end{pmatrix}N=\begin{pmatrix}0\\0\end{pmatrix}$$ Vi kan nu kigge på de resterende 3 krafter, som skal give ligevægt. $$\overrightarrow{w}+\overrightarrow{T_{3}}+\overrightarrow{T_{4}}=\begin{pmatrix}0\\0\end{pmatrix}$$ Nu kan vi se tilbage på eksemplet med maleriet (eks. 3) Det er samme situation (3 vektorer, hvor 2 er lige store, mens at den sidste er en tyngdekraft med kun y-komponent), og vi skal derfor bruge samme fremgangsmåde (evt. se eks. 3) $$sin(\theta)=\frac{\dfrac{\left|\overrightarrow{w}\right|}{2}}{\left|\overrightarrow{T_{3}}\right|}$$$$\implies\sin(45)=\frac{\dfrac{1000N}{2}}{\left|\overrightarrow{T_{3}}\right|}$$ $$\implies\left|\overrightarrow{T_{3}}\right|=\left|\overrightarrow{T_{4}}\right|=\frac{500N}{sin(45)}=707N$$  Ligesom i eks. 3, så er T₃ og T₄  halvdelen af tyngdekraftens størrelse: $$\overrightarrow{T_{y_3}}+\overrightarrow{T_{y_4}}+\overrightarrow{w_y}=\begin{pmatrix}0\\0\end{pmatrix}\implies\overrightarrow{T_{y_3}}=\overrightarrow{T_{y_4}}=\begin{pmatrix}0\\500\end{pmatrix}N$$

Nu skal x-komponenterne udregnes for T₃ og T₄:  $$\left|\overrightarrow{T_{x_3}}\right|=\left|\overrightarrow{T_{x_4}}\right|=\left|\overrightarrow{T_3}\right|\cdot\cos(\theta)\rightarrow\left|\overrightarrow{T_{x_3}}\right|=707N\cdot\cos(45)=500N$$ Dvs. vi har et system i ligevægt (mellem de 3 krafter), når $$\overrightarrow{w}=\begin{pmatrix}0\\-1000\end{pmatrix}N$$$$\overrightarrow{T_{3}}=\begin{pmatrix}500\\500\end{pmatrix}N$$$$\overrightarrow{T_{4}}=\begin{pmatrix}-500\\500\end{pmatrix}N$$

$$\implies\begin{pmatrix}0\\-1000\end{pmatrix}N+\begin{pmatrix}500\\500\end{pmatrix}N+\begin{pmatrix}-500\\500\end{pmatrix}N=\begin{pmatrix}0\\0\end{pmatrix}$$ Vi kan nu se, at hele systemet er i ligevægt: $$\overrightarrow{w}+\overrightarrow{T_{1}}+\overrightarrow{T_{2}}+\overrightarrow{T_{3}}+\overrightarrow{T_{4}}=\begin{pmatrix}0\\0\end{pmatrix}$$$$\begin{pmatrix}0\\-1000\end{pmatrix}+\begin{pmatrix}500\\500\end{pmatrix}+\begin{pmatrix}-500\\500\end{pmatrix}+\begin{pmatrix}200\\0\end{pmatrix}+\begin{pmatrix}-200\\0\end{pmatrix}=\begin{pmatrix}0\\0\end{pmatrix}$$