Brøker

Kære forælder

På denne side kan du læse om regnestrategier, men hvis det er første gang, du besøger vores side, vil anbefale, at du læser en af vores artikler først. Der er nemlig mange måder, du kan hjælpe dit barn med matematik, og de fleste måder handler ikke direkte om matematik.

Hvad er en brøk?

Det er ikke så enkelt at svare på, hvad en brøk er. Vi bruger brøker i mange forskellige situationer i hverdagen. Når vi taler om en halv time, en kvart liter fløde eller at vi er halvvejs, så bruger vi brøker.

En brøk er en særlig måde at skrive et tal, som ikke kan skrives som et helt tal. Vi skriver det op som to tal under hinanden adskilt af en vandret streg. Det øverste tal kalder vi tælleren, det nederste nævneren og stregen hedder en brøkstreg.

Man kan forstå brøker på flere forskellige måder:

1. Brøker er en måde at beskrive en del ud af en mængde af ting.
Der er 5 æbler, og du spiser 2 af dem. Du har nu spist 2 ud af 5, hvilket vi også kan skrive som brøken \( \frac{2}{5} \) (to femtedele).

2. Brøker er en måde at beskrive en del ud af en helhed.
Brøken \( \frac{2}{5} \) (to femtedele) kan også betyde en del af én ting, som er delt op i lige store stykker. Fx en kage, der er delt op i fem stykker, hvor to af stykkerne er blevet spist. Det væsentlige er, at der er 1 kage og ikke 5 kager som i ovenstående forståelse.

3. Brøker er tal.
En brøk er et tal, der kan placeres på en tallinje. Fx ligger brøken \( \frac{1}{2} \) (en halv) lige mellem 0 og 1. På den måde beskriver brøker nogle tal, der ligger mellem hele tal. På samme måde kan \( \frac{2}{5} \) (to femtedele) placeres på en tallinje sådan her:

Når brøker forstås på denne måde, behøver nævneren ikke at være størst. Fx er brøken \( \frac{12}{5} \) (tolv femtedele) større end 1. På nedenstående tallinje har vi markeret både \( \frac{2}{5} \) og \( \frac{12}{5} \). Læg mærke til at tallinjen går op til 3.

4. Brøker er en måde at skrive division på.
Når man skriver \( \frac{2}{5} \) (to femtedele), så er det en måde at skrive et divisionsstykke på, som man ikke har udregnet endnu. I dette tilfælde betyder det, at 2 skal divideres med 5.

5. Brøker er en måde at skrive et forhold på
Det kender vi fra nyheder med udsagn som ”2 ud af 5 danskere cykler med cykelhjelm”. Det betyder ikke, at der kun er 5 danskere, men udtrykker et forhold mellem dem, der bruger cykelhjelm og alle danskere, der cykler. Vi kender det også fra saftevand, der skal blandes 1:5. Her er brøkstregen erstattet af et kolon, men det betyder det samme som \( \frac{1}{5} \) (en femtedel).

Brøker kan altså forstås som: En del af mængde, en del af helhed, et tal, division og et forhold.

Forståelse af brøker afhænger af konteksten, men alle disse 5 forskellige måder skal være på plads, før man har fuldstændig styr på brøker. Det er derfor helt naturligt, hvis dit barn roder rundt i de mange forståelser.

Hvorfor skal man lære om brøker?

Brøker optræder mange steder i vores hverdag, fx bruger vi ordene kvart og halv ofte. Udover at tale om brøker og kunne regne med brøker, er det også væsentligt, at dit barn får en fornemmelse for forhold mellem tal (den 5. forståelse for brøker). Her er brøker uundværlige.

Hvis et barn donerer 20 kr. af sine lommepenge på 100 kr., er det relativt mere, end hvis en voksen donerer 100 kr. af sin løn.

Fordi vi kan beskrive verden mere præcist

Brøker er nødvendige for at kunne beskrive verden mere præcist, end man kan med hele tal. Et simpelt eksempel kunne være, at vi gerne vil undersøge, hvor mange der går til en fritidsaktivitet på 6. årgang. Der er to klasser på årgangen og resultatet af vores undersøgelse er, at 13 elever i 6A og 11 elever i 6B går til en fritidsaktivitet. Den information alene er ikke nok til, at vi kan sammenligne de to klasser, for vi mangler at beskrive det i forhold til, hvor mange elever der er i hver klasse i alt. Hvis vi ved at der er 27 elever i 6A og 22 elever i 6B, kan vi opskrive brøkerne for, hvor mange i hver klasse, der går til fritidsaktivitet:

I 6A går \(\frac{13}{27}\) til fritidsaktiviteter.

I 6B går \(\frac{11}{22}\) til fritidsaktiviteter.

Hvis vi skifter fra at se brøkerne som forhold til at se dem som tal på en tallinje, kan vi sammenligne forholdet i de to klasser, fordi vi kan se hvor stor en del ud af hele klassen, der går til en fritidsaktivitet.

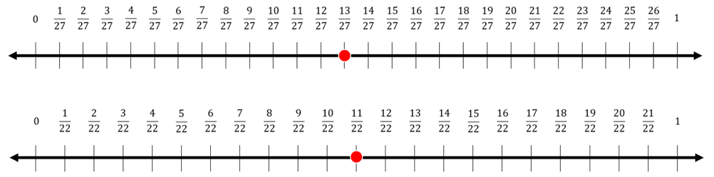
Ved at anvende brøker kan vi få et nyt perspektiv på sammenligningen af de to klasser. Selvom der er flere elever i 6A, der går til fritidsaktiviteter, viser det sig, at der er en større del af elever i 6B, der går til fritidsaktiviteter.

Fordi brøker er uundværlige

Brøker anvendes i mange grene af matematikken og gør os i stand til at arbejde med mere avanceret matematik. Eksempelvis bruges brøker i statistik og sandsynlighedsregning. Brøker er også uundværlige, når vi arbejder med ligninger, målestok og i overgangen til procentregning. Ligesom i skolens øvrige fag er det ikke altid tydeligt, hvad den nye viden kan bruges til, men skolens formål er heldigvis ikke altid at svare på, hvad viden skal anvendes til. Noget viden og nogle opdagelser er sejt i sig selv.

Typiske udfordringer med brøker

Dit barn kan opleve udfordringer med brøker flere gange i løbet af grundskolen. Udfordringerne opstår i forskellige situationer og knytter sig til nogle af de 5 forståelser for brøker, der er beskrevet ovenfor. Her er et udvalg af de typiske udfordringer dit barn kan møde:

Forvirring om størrelse

Når man arbejder med brøker som tal, så opfører de sig anderledes, end vi er vant til, at de hele tal gør. Indtil nu i skolelivet (og hverdagen) har dit barn været vant til, at man kan tælle - altså at der naturligt kommer et tal lige efter det tal, man lige har sagt. Men sådan er det ikke med brøkerne! Vi kan ikke på samme måde tælle brøkerne, for vi kan altid lave en anden brøk, der ligger lige mellem de to brøker, vi allerede har sagt. 

Når vi nu kan tælle de hele tal og sætte dem i rigtig rækkefølge, hvor fx 5 er større end 4, så er der mange børn, der synes, at det er forvirrende, at \(\frac{1}{5}\) (en femtedel) er mindre end \(\frac{1}{4}\) (en fjerdedel).

Hvad kan du som forælder kigge efter?

Hvis du skal finde ud af, om dit barn har problemer med at forstå størrelsen af brøker, så kan du fx stille dit barn følgende spørgsmål eller holde øje med følgende ting:

• Bytter dit barn rundt på, hvilken brøk der er størst?
• Har dit barn problemer med at sætte brøker ind på en tallinje?

Hvordan kan du som forælder hjælpe?

• Kig i dit barns matematikbog sammen med dit barn, så kan du bruge de samme tegninger/diagrammer som dit barn er vant til. 
• Du kan hjælpe dit barn med, hvordan man sætter brøker ind på en tallinje. Fx hvis vi skal placere \(\frac{2}{5}\) og \(\frac{1}{4}\), så starter vi med at dele tallinjen (fra 0 til 1) op i 5 lige store dele. Derefter markerer vi der, hvor 2 af disse dele slutter, så har vi nemlig fundet \(\frac{2}{5}\).
  Bagefter deler vi den samme tallinje (fra 0 til 1) op i 4 lige store dele og markerer der, hvor 1 del slutter - så har vi nemlig fundet \(\frac{1}{4}\).
  Nu bør det være nemt at se, hvilken brøk der er størst. 
  
  

Hjælp dit barn med at tegne brøkerne. Du skal dog være opmærksom på, at det med at tegne brøkerne også kan forvirre, når man skal regne med dem (se afsnittet ‘Diagrammer kan forvirre’). De fungerer dog fint til at få en fornemmelse for størrelsen på en enkelt brøk.
Her har vi fx tegnet \(\frac{1}{5}\) og \(\frac{1}{4}\) i cirkeldiagrammer.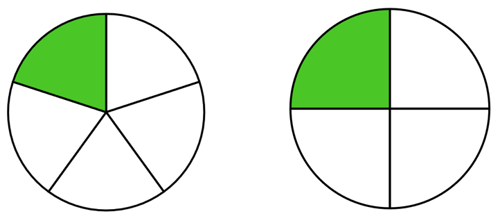

Hvis vi tager brøkdelene ud af diagrammerne, kan vi nemt se, at \(\frac{1}{4}\) er størst.

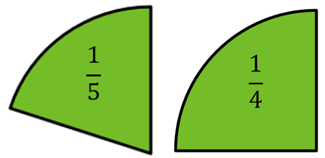
To brøker kan være samme tal

Indtil videre har dit barn lært, at alle tal er unikke. Altså to forskellige tal, kan ikke have samme værdi eller betyde det samme. 2 er ikke det samme som 5. Det ændrer sig, når dit barn skal lære om brøker. Brøker kan nemlig beskrive forhold. Og det samme forhold kan godt beskrives på flere forskellige måder.

Et simpelt eksempel er brøkerne \(\frac{1}{4}\) (en fjerdedel) og \(\frac{2}{8}\) (to ottendedele). Tælleren og nævneren i de to brøker er ikke ens. Men hvis vi sætter brøkerne på en tallinje, vil de sidde nøjagtig samme sted. Eller hvis vi udregner divisionsstykkerne, vil de begge give 0,25.

Det kan naturligvis skabe en del forvirring, fordi dit barn pludselig skal til at arbejde med, at forskellige brøker kan repræsentere det samme. Vi har også brøk-operationer, der arbejder med at skifte mellem forskellige repræsentationer af det samme tal. Det kalder vi at forkorte og forlænge brøker. Det sker ved, at man ganger eller dividerer både tæller og nævner i en brøk med det samme tal. Så længe man udfører den samme operation på både tæller og nævner, vil den nye brøk stadig repræsentere det samme tal.

Hvis vi starter med brøken (\frac{1}{4}\), så kan vi fx gange både tæller og nævner med 2.

$$ \frac{1}{4} = \frac{1\cdot 2}{4\cdot 2} = \frac{2}{8} $$

Så har vi forlænget brøken med 2 og fået den nye brøk \(\frac{2}{8}\) . Tæller og nævner er begge nye tal, men brøken \(\frac{2}{8}\) repræsenterer det samme tal som den oprindelige brøk, \(\frac{1}{4}\) .

Hvad kan du som forælder kigge efter?

• Har dit barn svært ved at acceptere at to forskellige brøker kan være samme forhold? Fx hvis de siger at \(\frac{10}{20}\) (ti tyvendedele) er større end \(\frac{1}{2}\) (en halv) fordi 10 er større end 1.

Hvordan kan du som forælder hjælpe?

• At forkorte og forlænge brøker er knyttet til en forståelse af brøker som kan tage mange år at opnå. Hav tålmodighed og stol på at dit barn nok skal lære det i skolen.
  
  
• Du kan eventuelt hjælpe dit barn med at sammenligne størrelser på brøker på samme måde som vi har gjort på denne temaside ved at tegne tallinjer eller diagrammer.

Diagrammer kan forvirre

En anden udfordring handler om de tegninger, vi viser børnene. Tegningerne bruges i bedste mening og kan være en stor hjælp, men man skal være forsigtig. Nogle tegninger kan nemlig forstærke visse misforståelser. Her er et eksempel:

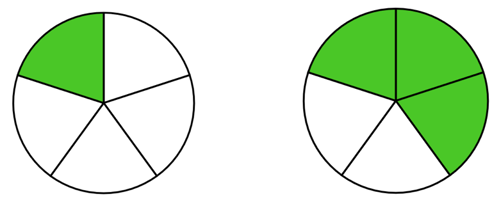
Diagrammet til venstre viser \( \frac{1}{5} \) (en femtedel) og diagrammet til højre viser \( \frac{3}{5} \)  (tre femtedele). Diagrammerne i sig selv er ikke et problem. Problemet opstår når vi skal regne med brøker. Hvad sker der for eksempel når brøker lægges sammen? I ovenstående tilfælde viser de to diagrammer tilsammen \( \frac{1}{5} + \frac{3}{5} = \frac{4}{5} \)  (fire femtedele). Men nogle børn læser diagrammerne anderledes. Børnene ser, at der er 10 felter i alt og at fire af dem har farve. De tror altså at diagrammerne viser \( \frac{4}{10} \)  (fire tiendedele) og kan komme til at tro at \( \frac{1}{5} + \frac{3}{5} = \frac{4}{10} \), hvilket ikke er rigtigt. Denne forvirring opstår gerne fordi børnene kun er nået til forståelse nummer 1 i listen fra afsnittet ”Hvad er en brøk?”.

Hvad kan du som forælder kigge efter?

• Kan dit barn skrive en brøk med symboler ud fra diagrammer?
• Er dit barn primært forvirret når der er flere diagrammer eller brøker?

Hvordan kan du som forælder hjælpe?

• At ovenstående diagrammer kan forvirre, handler om at børnene tæller alle felterne, men faktisk bør de bare tælle de farvede felter og huske, at ét felt svarer til \( \frac{1}{5} \). Der er 4 felter, der svarer til \( \frac{1}{5} \) hver, altså fire femtedele.
  
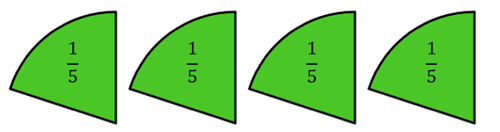
  Som forælder kan du altså hjælpe med at tegne brøkdelene i stedet for hele cirkeldiagrammer når det handler om at regne med brøker.
• Dig og dit barn kan også tegne mange forskellige typer diagrammer. Her kan du se nogle andre diagrammer, der særligt handler om at regne med brøker.

Ægte og uægte brøker

De første brøker dit barn lærer, er typisk det vi kalder ægte brøker. I ægte brøker er tælleren mindre end nævneren, fx \( \frac{1}{2} \) eller \( \frac{1}{4} \) eller \( \frac{7}{18} \). Alle ægte brøker svarer til et tal mellem 0 og 1 når vi skal placere dem på en tallinje.

Fordi der bruges lang tid på ægte brøker i skolen, er der mange børn, der tror, at tælleren altid skal være mindre end nævneren, men sådan er det ikke. Fx er \( \frac{12}{5} \) også en brøk. Brøker, hvor tælleren er større end nævneren kaldes nogle gange for uægte brøker.

Hvad kan du som forælder kigge efter?

• Har dit barn svært ved at acceptere at brøker kan være større end 1?
• Kan dit barn placere uægte brøker på en tallinje?

Hvordan kan du som forælder hjælpe?

• Brug sætninger som ”filmen varer halvanden time” eller ”det tager fem kvarter at køre derhen”. På den måde bliver dit barn opmærksom på, at man kan betegne noget, der er større end 1 ved hjælp af brøkdele.
  
  
• Klip eventuelt brøkdele ud i papir. Fx femtedele
  
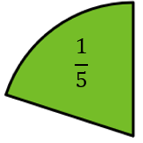
  Klip mere end fem ud og se at det danner mere end 1 hel cirkel.
  
  
• Prøv at placér en uægte brøk på en tallinje. Hvilket helt tal kommer I tættest på? Fx er \( \frac{12}{5} \) større end 2, men mindre end 3. Brug eventuelt en lommeregner og regn brøken som division.

Når brøker blandes med regning

Når dit barn skal til at lære om at bruge plus, minus, gange og dividere sammen med brøker, bliver emnet ofte svært. Du husker måske selv noget med at finde en fælles nævner. Følgende side handler om brøkregnereglerne. Kig eventuelt på reglerne og diagrammerne sammen med dit barn.