Ugrupperede vs. Grupperede
Der findes overordnet set to slags observationer: ugrupperede og grupperede.
I dette afsnit ser vi på, hvad forskellene er på dem. I de senere afsnit vil vi dele op og se på dem hver for sig, når det er nødvendigt.
Når vi har et datasæt, er data som udgangspunkt ikke grupperet. Det er op til os at vurdere, om det giver mening at gruppere datasættet i netop dette tilfælde. Når man grupperer et datasæt, inddeler vi observationerne i intervaller.
Et godt billede til at skelne er, om man måler folks skostørrelse eller højde.
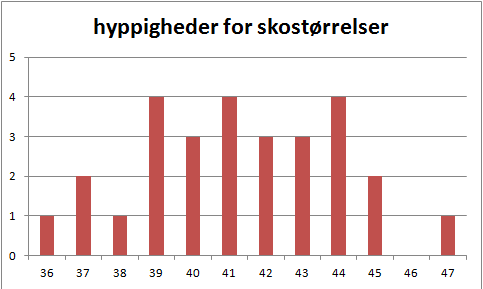
Ved skostørrelse vil du observere 36, 37, 38, 39, … , 44, 45, 46, 47. Der er altså tale om ugrupperede observationer, hvor der ikke er så mange forskellige observationer, og hvor hyppigheden af hver observation ofte er større end 1. Vi kan godt gruppere data, men så ville data ikke være lige så detaljeret, som vi måske kunne ønske os. Ved at tegne et diagram over data, får vi fint overblik, selvom data ikke er grupperet.
Ved højder er der mange flere muligheder. Man kunne f.eks. forestille sig, at få højderne 165,4, 187,38, 176,7. De fleste ville forekomme med hyppighed 1. Derfor er det smartere at samle dem i intervaller. F.eks. ]160;165], ]165,170], …, ]185,190], ]190,195].
Her har vi altså valgt at gruppere vores data, fordi det giver det bedste overblik.
Ved grupperede observationer taler man om intervalhyppighed og intervalfrekvens, svarende til hvor mange observationer der falder indenfor hvert interval og hvor stor en procentdel af observationerne der falder inden for hvert interval.
Søjlediagrammer og histogrammer
Når man skal lave en oversigt over, hvordan observationerne fordeler sig, gør man det forskelligt alt efter om der er tale om grupperede eller ugrupperede observationer.
Ved ugrupperede observationer, vil man typisk tegne et søjlediagram. Man har observationerne henad x-aksen, og for hver observation sætter man en lodret søjle, der enten markerer hyppigheden eller frekvensen for denne observation.
For grupperede observationer kan man ikke lave søjlediagrammer. I stedet laver man såkaldte histogrammer.
Et histogram har intervalgrænserne på x-aksen. På y-aksen er der imidlertid ikke angivet nogen akseværdier. Den måde man aflæser et histogram på er nemlig ved at se på arealet af hver søjle. Øverst i højre hjørne er angivet hvor stort et areal 5% svarer til. Hvis man lægger arealerne af søjlerne sammen, får man 100%.
Hvis intervallerne har samme bredde, svarer søjlernes højde til intervalhyppigheden. Men det er ikke altid, at alle intervallerne har samme bredde. Nedenfor er tegnet to histogrammer, der repræsenterer de samme observationer. I det første histogram har alle intervallerne bredde 5, mens det i det andet varierer mellem intervalbredder af 5 og 10.
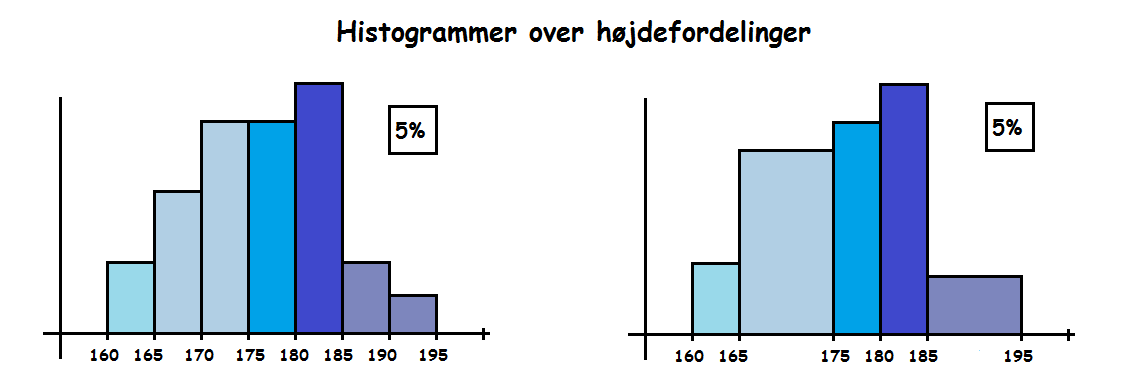
Når man slår to søjler sammen, skal man altså sørge for, at den nye søjle har samme areal som de to tidligere havde tilsammen.
