Cosinusrelationerne
Ofte kommer man ud for opgaver, hvor man i en trekant kender nogle sider og vinkler og bliver bedt om at finde nogle andre sider eller vinkler. Til at løse den slags opgaver er cosinusrelationerne et stærkt værktøj.
Det, der gør cosinusrelationerne til et stærkt redskab, er, at de gælder i vilkårlige trekanter. Det er altså ligegyldigt, om den trekant, vi arbejder med, er retvinklet, ligebenet, ligesidet eller ingen af delene. Vi kan bruge cosinusrelationerne til dem alle sammen. Klik her for at se et eksempel på, hvor cosinusrelationerne kan bruges i virkeligheden.
Hvis man vil finde en side
Hvis man kender to sider og den vinkel, der er imellem siderne, kan man bruge cosinusrelationerne til at finde længden af den tredje side. Det gør man på følgende måde:
$$a^2=b^2+c^2-2bc\cos(A)$$
$$b^2=a^2+c^2-2ac\cos(B)$$
$$c^2=a^2+b^2-2ab\cos(C)$$
Grunden til de tre formler er, at det kommer an på hvilke sider, man kender, og hvilken, man vil finde.
Læg mærke til, at formlerne minder en del om Pythagoras' læresætning, hvor der blot er tale om et ekstra led.
Det kan være svært at huske disse formler udenad. En god huskeregel er dog, at siden til venstre har samme bogstav som vinklen til højre, man skal tage cosinus til.
Eksempel:
Vi bliver bedt om at finde siden a i denne trekant
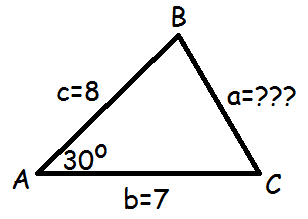
Da vi kender vinkel A og siderne b og c, er det den øverste formel, vi skal bruge.
$$a^2=b^2+c^2-2bc\cos(A)$$
$$a^2=7^2+8^2-2\cdot7\cdot8\cdot\cos(30^\circ)$$
$$a^2=49+64-112\cdot0,866$$
$$a^2=16,01$$
$$a=\sqrt{16,01}\approx4$$
Hvis man vil finde en vinkel
Hvis man kender alle tre sider i en trekant, og man ønsker at finde en vinkel, kan man bruge følgende formler
$$\cos(A)=\frac{b^2+c^2-a^2}{2bc}$$
$$\cos(B)=\frac{a^2+c^2-b^2}{2ac}$$
$$\cos(C)=\frac{a^2+b^2-c^2}{2ab}$$
Formlerne er faktisk præcist de samme som ovenfor, hvor man bare har isoleret cosinus til vinklen i stedet for en af siderne. Neden for ser vi, hvordan man kommer fra en af de tre øverste fomler til en af de tre nederste. Farverne markerer hvilke ting, vi har rykket rundt på.
$$a^2=b^2+c^2{\color{Red} {-2bc\cos(A)}}$$
$${\color{Blue}{ a^2}}+{\color{Red} {2bc\cos(A)}}=b^2+c^2$$
$${\color{Cyan} {2bc}}\cos(A)=b^2+c^2{\color{Blue}{-a^2}}$$
$$\cos(A)=\frac{b^2+c^2-a^2}{{\color{Cyan} {2bc}}}$$
Lad os tage et eksempel.
Vi ønsker at finde vinkel B i følgende trekant
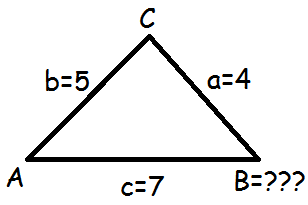
Da det er vinkel B, vi ønsker at finde, bruger vi formel nummer to i rækken.
$$\cos(B)=\frac{a^2+c^2-b^2}{2ac}$$
$$\cos(B)=\frac{4^2+7^2-5^2}{2\cdot4\cdot7}$$
$$\cos(B)=\frac{16+49-25}{56}$$
$$\cos(B)=\frac{40}{56}=\frac{5}{7}\approx0,714$$
Nu ved vi, hvad cos(B) er, men vi blev bedt om at finde selve B. Derfor tager vi cos-1 på begge sider.
$$\cos(B)=0,714$$
$$B=\cos^{-1}(0,714)$$
$$B=44,42^\circ$$
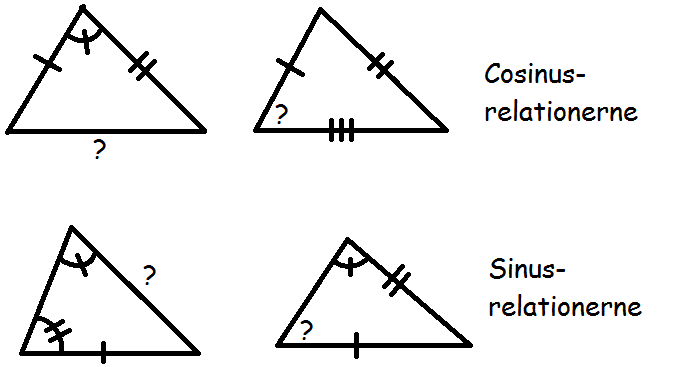
Skal jeg bruge cosinus- eller sinusrelationerne?
Her er en oversigt over, hvornår det er smartest at bruge hhv. cosinus- og sinusrelationerne. De vinkler og sider, der er markeret med streger, er de ting, vi kender på forhånd. Spørgsmålstegnene markerer de sider eller vinkler, vi er interesserede i at finde.