Determinant
Når man har to vektorer kan man finde deres determinant. Man får determinanten ved at hatte den første vektor og prikke med den anden.
$$\det(\overrightarrow{a},\overrightarrow{b})=\hat{\overrightarrow{a}}\cdot\overrightarrow{b}=a _1b_2-a_2b_1$$
Der findes to måder at notere determinanten på. Enten ved at skrive det eller også ved at skrive de to vektorers koordinater op i et skema som vist nedenfor. Her betyder de lodrette streger altså hverken "længde" eller "numerisk værdi" men i stedet "determinant".
$$\det(\overrightarrow{a},\overrightarrow{b})=\begin{vmatrix}a_1 & b_1 \\a_2 & b_2\end{vmatrix}$$
Hvis man skriver determinanten op på den sidste måde, er den let at regne ud. Man skal nemlig bare gange over kryds.
Først ganger man øverste venstre med nederste højre, hvorfra man trækker nederste venstre ganget med øverste højre.
$$\begin{vmatrix}{\color{Red} {a_1}} &{\color{Blue}{ b_1}} \\{\color{Blue} {a_2}} & {\color{Red}{ b_2}}\end{vmatrix}={\color{Red}{ a_1b_2}}-{\color{Blue} {a_2b_1}}$$
F.eks. hvis
$$\overrightarrow{a}=\begin{pmatrix}3\\2\end{pmatrix},\overrightarrow{b}=\begin{pmatrix}1\\5\end{pmatrix}$$
så er
$$\det(\overrightarrow{a},\overrightarrow{b})=\begin{vmatrix}3 & 1\\2 & 5\end{vmatrix}=3\cdot5-2\cdot1=13$$
Areal og determinant
Determinanten af to vektorer er et tal. Den numeriske værdi af dette tal svarer til arealet af det parallelogram, som de to vektorer udspænder.
$$A_{parallelogram}=|\det(\overrightarrow{a},\overrightarrow{b})|$$
$$A_{parallellogram}=\begin{Vmatrix}a_1 & b_1\\a_2 & b_2\end{Vmatrix}\\$$
Her skal man igen være lidt opmærksom på de lodrette streger. De yderste betyder "numerisk værdi", mens de inderste betyder "determinant".

Hvis vi f.eks. ønsker at finde arealet af parallelogrammet udspændt af vektorerne
$$\overrightarrow{a}=\begin{pmatrix}1\\4\end{pmatrix},\overrightarrow{b}=\begin{pmatrix}3\\2\end{pmatrix}$$
så kan det beregnes således:
$$A_{parallelogram}=|\det(\overrightarrow{a},\overrightarrow{b})|=\begin{Vmatrix}1 & 3\\4 & 2\end{Vmatrix}=|1\cdot2-4\cdot3|=|-10|=10$$
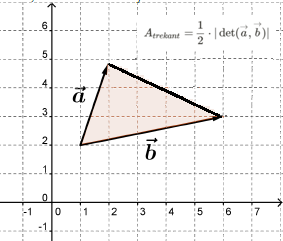
Arealet, der udspændes mellem de to vektorer, er halvt så stort som arealet af parallelogrammet. Derfor kan arealet af trekanten med formlen:
$$A_{trekant}=\frac{1}{2} \cdot |\det(\overrightarrow{a},\overrightarrow{b})|$$
Parallelle vektorer og determinant
Hvis determinanten af to vektorer er 0, så er vektorerne parallelle. Skrevet matematisk er det:
$$\det(\overrightarrow{a},\overrightarrow{b})=0\quad\Leftrightarrow\quad\overrightarrow{a}\parallel\overrightarrow{b}$$
Grunden til dette er, at determinanten er defineret som skalarproduktet mellem a hat og b. Hvis dette skalarprodukt giver 0, betyder det at de to vektorer står vinkelret på hinanden. Hvis b er vinkelret på a hat, så er b parallel med a.

Bemærk, at hvis a og b er parallelle, så kan de enten være ensrettede eller modsatrettede.
Lad os tage et eksempel. Vi skal afgøre om vektorerne
$$\overrightarrow{a}=\begin{pmatrix}3\\2\end{pmatrix}\text{ og }\overrightarrow{b}=\begin{pmatrix}-1\\7\end{pmatrix}$$
er parallelle.
Vi ser at
$$\det(\overrightarrow{a},\overrightarrow{b})=\begin{vmatrix}3 & -1\\2 & 7\end{vmatrix}=3\cdot7-2\cdot(-1)=23\neq0$$
Da determinanten er forskellig fra 0, er de to vektorer ikke parallelle.
