Materialeberegning: areal
Uanset hvilket byggeprojekt der arbejdes på - om der skal bygges store villaer eller små skure - skal der anvendes materialer. Men hvordan finder vi præcist ud af, hvor stor en mængde materialer, der skal anvendes? Mængden af materialer hænger sammen med, hvordan de skal anvendes, og dermed hvilken form, de skal anvendes i.
Hvis der f.eks. skal opsættes loftplader, ligesom i videoen ovenfor, afhænger antallet af loftplader af loftets størrelse. På samme måde gælder det, at mængden af træ til en tagkonstruktion afhænger af tagets form og størrelse, ligesom at antallet af gipsplader til en væg afhænger af væggens bredde og højde. Derfor er vi nødt til at kigge på arealet af de forme, der skal konstrueres, for at vi kan finde ud af, hvor meget materiale, der skal anvendes.
Nedenfor gennemgår vi eksempler på, hvordan areal anvendes ved byggeprojekter til at beregne mængden af materialer. Ligesom der bliver nævnt i videoen ovenfor, er målene for f.eks. et loft eller en væg typisk givet på en tegning, som ofte er tegnet i et målestoksforhold. Et af eksemplerne omhandler derfor også, hvordan mængden af materialer beregnes ud fra en tegning angivet i et målestoksforhold. Skulle du undervejs blive i tvivl om, hvor formlerne til beregning af areal kommer fra, eller hvad målestoksforhold betyder, kan du læse vores sider om areal og målestoksforhold, hvor disse emner er beskrevet. Inden eksemplerne gennemgår vi dog en enkelt huskeregel om areal.
Areal er et udtryk for hvor meget noget fylder på en flad overflade. Lejligheder og rum er f.eks. typisk angivet i m2. Gulv er f.eks. en flad overflade, og hvis vi har fået oplyst at en lejlighed er på 50 m2, betyder det altså at der er 50 m2 gulvplads. På samme måde kan væggene i et rum udgøre f.eks. 20 m2, eller en træplade kan have et areal på 1 m2, og vi kan få til opgave at skære den ud i mindre lige store plader med et areal på 10 cm2.
Nu er vi klar til eksemplerne
Eksempler
1: Opsætning af vægge
Der skal opsættes gipsplader i 2 lag til væggene i et rum. Rummet er formet som et rektangel, med den lange side på 5 m og den korte side på 3 m. Væggene er overalt 2,3 m høje. Arealet af døren til rummet udgør 1,68 m2. Gipspladerne måler 0,9 m \( \times \) 2,4 m. En tegning af rummet kan ses nedenfor.
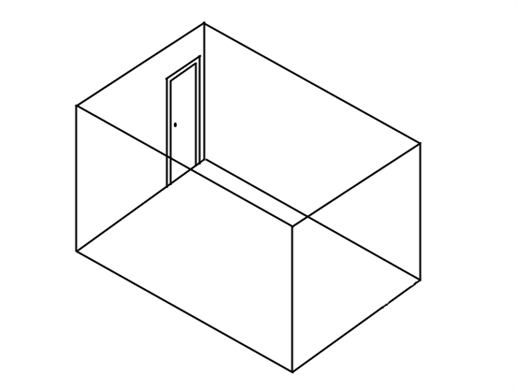
Opgaven lyder på at beregne hvor mange gipsplader, der skal anvendes.
Hvis vi udregner væggenes areal, og udregner arealet af én gipsplade, kan vi dividere væggenes areal med gipspladens. På denne måde kan vi finde ud af, hvor mange gipsplader, der skal til, så hele væggenes areal er dækket af gipsplader. Vi skal også tage højde for, at der ikke skal opsættes gipsplader, der hvor døren skal være. Men det vender vi tilbage til.
Rummet er formet som et rektangel, men vi kan også se hver væg som et rektangel. Arealet af et rektangel beregnes ved at gange længden af siderne sammen. Arealet af en kort og en lang væg bliver derfor:
$$ \mathrm{areal}_{kort \ væg} = 3 m \cdot 2,3 m = 3\cdot 2,3 m^2 = 6,9 m^2 \\
\mathrm{areal}_{lang \ væg} = 5 m \cdot 2,3 m = 5 \cdot 2,3 m^2 = 11,5 m^2 $$
Da vi har to korte og to lange vægge, bliver det samlede areal af væggene derfor:
$$ \mathrm{areal}_{vægge} = (2 \cdot 6,9 m^2) + (2\cdot 11,5 m^2) =13,8 m^2 + 23 m^2 = 36,8 m^2 $$
Men vi skal som nævnt ikke sætte gipsplader op, hvor der skal være en dør. Vi bliver derfor nødt til at trække arealet af døren fra det samlede areal af væggene. Arealet af væggene, hvor der skal opsættes gipsplader, bliver derfor:
$$ \mathrm{areal}_{vægge} - \mathrm{areal}_{dør} = 36,8 m^2 - 1,68 m^2 = 35,12 m^2$$
Nu mangler vi bare at finde arealet af én gipsplade. Ligesom væggene, kan vi se gipspladen som et rektangel. Arealet bliver derfor:
$$ \mathrm{areal}_{plade} = 0,9 m \cdot 2,4 m = 9 \cdot 2,4 m^2 = 2,16 m^2$$
Vi dividere nu arealet af væggene med arealet af en gipsplade, for at finde antallet af gipsplader til ét lag.
$$ \mathrm{antal} \ \mathrm{plader}_{et \ lag} = \frac{\mathrm{areal}_{vægge}}{\mathrm{areal}_{plade}} = \frac{35,12 m^2}{2,16 m^2} = 16,26 $$
Men der skal opsættes to lag plader. Det samlede antal plader bliver derfor:
$$ 2 \cdot 16,26 = 32,52 $$
Da vi ikke kan bestille en halv plade, er vi nødt til at runde op. Der skal derfor i alt bruges 33 plader.
2: Målestoksforhold og gipsplader
Til et loft skal der monteres gipsplader. Hver gipsplade måler 0,95 m \( \times \) 2,3 m. En tegning af loftet er vist i målestoksforholdet 1:100 nedenfor.
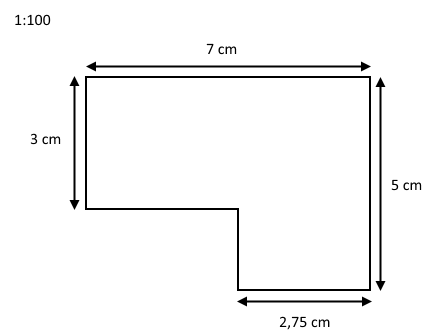
Opgaven lyder på at beregne hvor mange gipsplader, der skal anvendes til loftet.
Nøjagtigt som i Eksempel 1, skal vi beregne loftets samlede areal og dividere dette med arealet af én gipsplade, for at finde ud af, hvor mange gipsplader der skal til. Men da tegningen er angivet i et målestoksforhold, skal vi først omregne til loftetes virkelige mål. Vi henviser igen til vores side om målestoksforhold, hvis du bliver i tvivl undervejs. Da loftet har en form, som vi ikke direkte kan regne arealet af, inddeler vi loftet i to rektangler, som ses på tegningen nedenfor:
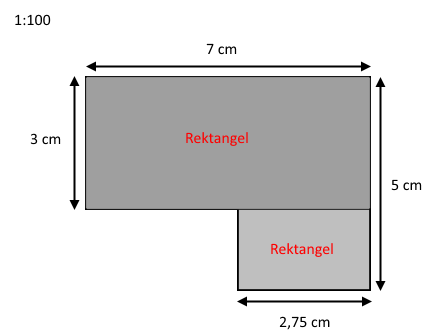
Vi udregner først arealet af det store rektangel. Da vi skal finde målene i virkeligheden, skal vi gange med målestoksforholdet. Vi får:
Kort side: \( 3 cm \cdot 100 = 300 cm = 3 m \)
Lang side: \( 7 cm \cdot 100 = 700 cm = 7 m \)
Arealet af et rektangel beregnes ved at ganges dets sider sammen. Det virkelige areal af det store rektangel bliver derfor:
$$ \mathrm{areal}_{stort \ rektangel} = 3 m \cdot 7 m = 3 \cdot 7 m^2 = 21 m^2 $$
Vi beregner nu arealet af det lille rektangel. Hvis vi ser på tegningen, er en af siderne for det lille rektangel 2,75 cm på tegningen. Samtidig kan vi se, at hvis vi trækker 3 cm (en af siderne på det store rektangel) fra de 5 cm, får vi præcis længden af det lille rektangels anden side. Rektanglets anden side udgør derfor 2 cm på tegningen. Vi omregner nu siderne til virkelige mål, og igen skal vi gange med målestoksforholdet:
Kort side: \( 2 cm \cdot 100 = 200 cm = 2 m \)
Lang side: \( 2,75 cm \cdot 100 = 275 cm = 2,75 m \)
Arealet af det lille rektangel bliver derfor:
$$ \mathrm{areal}_{lille \ rektangel} = 2 m \cdot 2,75 m = 2 \cdot 2,75 m^2 = 5,5 m^2 $$
Loftets samlede areal er derfor:
$$ \mathrm{areal}_{loft} = 21 m^2 + 5,5 m^2 = 26,5 m^2 $$
Vi mangler nu at udregne arealet af en gipsplade. Gipspladen kan vi også se som et rektangel, og arealet bliver derfor:
$$ \mathrm{areal}_{plade} = 0,95 m \cdot 2,3 m = 0,95 \cdot 2,3 m^2 = 2,185 m^2 $$
For at finde antallet af gipsplader, der skal anvenedes, skal vi dividere loftets samlede areal med arealet af en gipsplade.
$$ \mathrm{antal} \ \mathrm{plader} = \frac{\mathrm{areal}_{loft}}{\mathrm{areal}_{plade}} = \frac{26,5 m^2}{2,185 m^2} = 12, 13 $$
Igen kan vi ikke bestille plader, der ikke er hele, så der skal i alt anvendes 13 plader.
