Målestoksforhold

Når der arbejdes på store bygninger, er det praktisk at have en teknisk tegning af f.ek.s hvordan kabelføringen skal udføres, og hvor belysning og stikkontakter skal monteres. Forestil dig for eksempel dit lokale supermarked eller skole, hvor der typisk hænger stribevis af lamper i loftet. Det ville være ret upraktisk, hvis tegningerne af, hvor disse lamper skal placeres, skulle være lige så store som selve lokalerne, hvori de skal monteres. Derfor anvender man målestoksforhold. På den måde kan man tegne store og mange ting på små papirer, eller man kan forstørre små ting op. 

Nedenfor gennemgår vi, hvordan målestoksforhold anvendes i forbindelse med tekniske tegninger. Skulle du blive i tvivl undervejs om, hvad målestoksforhold betyder, eller hvor formlerne kommer fra, kan du læse vores side om målestoksforhold.
Inden vi går i gang med eksemplerne gennemgår vi dog nogle huskeregler om målestoksforhold. 

Hvis vi har fået en tegning angivet i målestoksforholdet \(1:100 \) betyder dette at "1 enhed på tegningen svarer til 100 enheder i virkeligheden". Hvis tegnigen f.eks. er angivet i cm betyder det altså at "1 cm på tegningen svarer til 100 cm i virkeligheden". 

Hvis vi skal finde radius af en rund loftlampe i virkeligheden, når vi kun har tegningen, kan vi også anvende målestoksforholdet. Hvis målestoksforholdet er \(1:100 \) og radius på tegningen er \(0,4 cm\), ganger vi med den del der svarer til "100 enheder i virkeligheden". Altså:
$$0,4 cm\cdot100 = 40 cm $$

Hvis vi omvendt bliver bedt om at skulle konstruere en teknisk tegning af lampen og derfor gerne vil vide, hvad dens radius skal være på tegningen, skal vi dividere med den del der svarer til "100 enheder i virkeligheden". Altså:
$$\frac{40 cm}{100}  = 0,4 cm $$

Nu er vi klar til eksemplerne.

Eksempler

1: Fra virkelighed til tegning

 Vi har fået givet følgende skitsetegning af et klasselokale, hvor der skal monteres loftlamper. Alle lamper har de samme mål.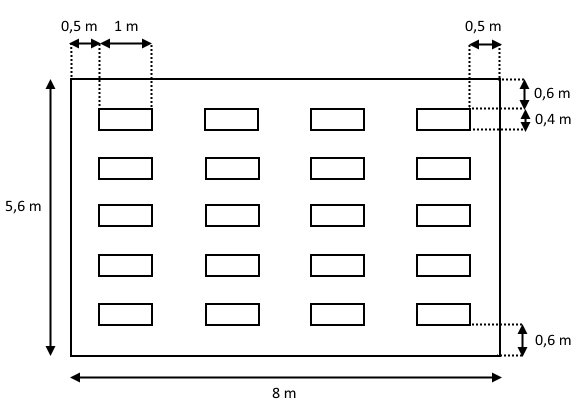 

Hver loftlampe (de firkantede kasser på tegningen) har en længde på 1 m og en bredde på 0,4 m. Opgaven lyder på at konstruere en tegning af klasselokalet og lamperne i målestoksforholdet \(1:100\). 

For at gøre det mere overskueligt farvelægger vi nogle af stregerne på tegningen: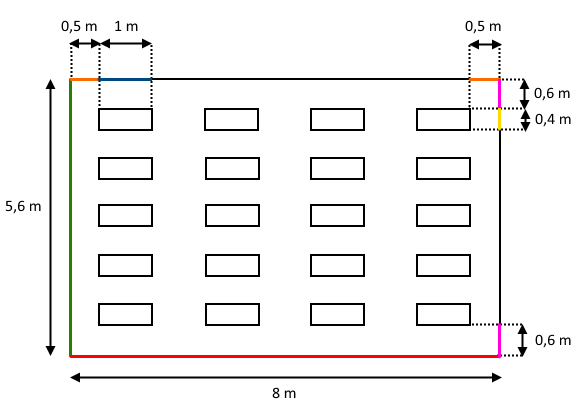

For at kunne tegne tegningen i målestoksforholdet, skal vi først vide hvad længde hver væg skal have på tegningen. Derfor dividerer vi med 100. 
Rød væg: \( \frac{8 m}{100} = 0,08 m = 8 cm \)
Grøn væg: \( \frac{5,6 m}{100} = 0,056 m = 5,6 cm \)
Her har vi brugt at 1 m  svarer til 100 cm. 

Næste skridt er at finde ud af, med hvilken afstand lamperne skal placeres fra hinanden. Vi starter med at se på afstanden mellem lampernes bredder (gul linje). På tegningen kan vi se, at lamperne langs den øverste væg og den røde væg, skal placeres med en afstand på 0,6 m (pink linje) fra disse vægge. Der er 5 lamper nedad fra den øverste væg til den nederste røde væg. Dette betyder, at vi ud fra tegningen kan se at, hvis lægger længderne af 5 gule linjer, længderne af 2 pink linjer og længderne af de 4 mellemrum mellem de gule linjer sammen, får vi, hvad der svarer til længden af den grønne væg. Altså:

\( (5 \cdot \mathrm{gul} \ \mathrm{linje}) + (2 \cdot \mathrm{pink} \ \mathrm{linje}) + (4 \cdot \mathrm{mellemrum}) = \mathrm{grøn} \ \mathrm{væg} \)
\((5 \cdot 0,4 m) + (2 \cdot 0,6 m) + (4 \cdot \mathrm{mellemrum}) = 5,6 m \)
\(4 \cdot \mathrm{mellemrum} = 5,6 m - (5 \cdot 0,4 m) - (2 \cdot 0,6 m) \)
\(\mathrm{mellemrum} = \frac{5,6 m - (5 \cdot 0,4 m) - (2 \cdot 0,6 m)}{4} \)
\(\mathrm{mellemrum} = \frac{2,4 m}{4} = 0, 6 m \)

Dette betyder at afstanden mellem lampernes bredder er 0,6 m, og samtidig skal lamperne langs den nederste røde væg og øverste væg placeres med samme afstand. På tegningen bliver dette:
Afstand til røde vægge og afstand mellem lampernes bredder:

\(\frac{0,6 m}{100} = 0,006 m = 0,6 cm = 6 mm \)
Hertil har vi brugt, at 1 cm svarer til 10 mm. 

Da vi nu har afstanden mellem lampernes bredder, skal vi nu finde afstanden mellem lampernes længder (blå linjer). På tegningen kan vi se, at lamperne langs den grønne væg og væggen til højre skal placeres med en afstand på 0,5 m til disse vægge. Der 4 lamper henad fra den grønne væg til den højre væg. Dette betyder, at vi ud fra tegningen kan se at, hvis vi lægger længderne af 4 blå linjer, længderne af 2 orange linjer og længderne af de 3 mellemrum mellem de blå linjer sammen, får vi, hvad der svarer til længden af en rød væg. Altså:

\( (4 \cdot \mathrm{blå} \ \mathrm{linje}) + (2 \cdot \mathrm{orange} \ \mathrm{linje}) + (3 \cdot \mathrm{mellemrum}) = \mathrm{rød} \ \mathrm{væg} \)
\((4 \cdot 1 m) + (2 \cdot 0,5 m) + (3 \cdot \mathrm{mellemrum}) = 8 m \)
\(3 \cdot \mathrm{mellemrum} = 8 m - (4 \cdot 1 m) - (2 \cdot 0,5 m) \)
\(\mathrm{mellemrum} = \frac{8 m - (4 \cdot 1 m) - (2 \cdot 0,5 m)}{3} \)
\(\mathrm{mellemrum} = \frac{3 m}{3} = 1 m \)

Dette betyder, at afstanden mellem lampernes længder er 1 m, og samtidig skal lamperne langs den grønne væg og væggen til højre placeres med en afstand 0,5 m til væggene. På tegningen bliver dette:

Afstand til grøn og højre væg: \( \frac{0,5 m}{100} = 0,005 m = 0,5 cm  = 5 mm \)
Afstand mellem lampernes længder: \( \frac{1 m}{100} = 0,01 m = 1 cm  \)

Til slut mangler vi blot at udregne, hvad længden og bredde på hver lampe skal være på tegningen. Da lamperne på skistetegningen har en længde på 1 m, har vi allerede udregnet ovenfor, hvad dette bliver på målestokstegnigen. For lampens bredde får vi:
Bredde af en lampe: \( \frac{0,4 m}{100} = 0,004 m = 0,4 cm = 4 mm \)

Den endelige tegning bliver da: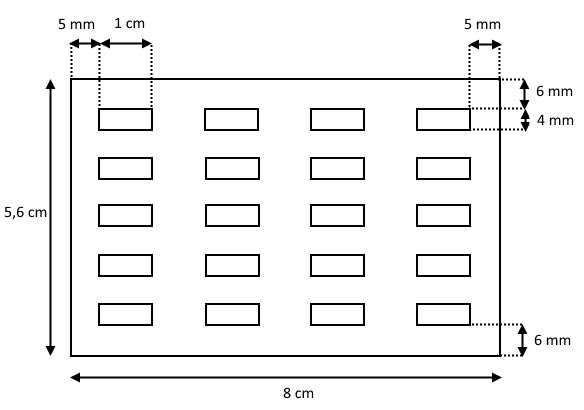 

2: Fra tegning til virkelighed

Nedenfor er vist en tegning i målestoksforholdet \( 1: 25 \).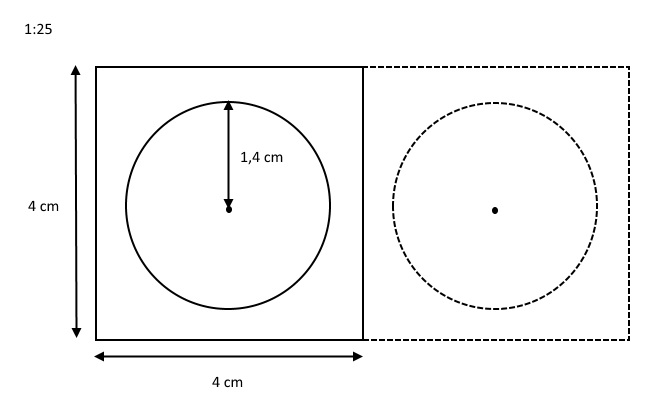

Tegningen forestiller to gipsplader (kvadrater) samt to runde lamper (cirkler), der skal monteres i loftet. Vi forestiller os, at den venstre del af tegningen (tykke streger) allerede er blevet monteret. Lampen er monteret, så dens centrum præcis er i gipspladens centrum. Nu vil vi gerne montere højre gipsplade og lampe (stiplede streger) på præcis samme måde. Opgaven lyder nu på at finde ud af, hvor langt der er fra den montrede lampes centrum hen til næste lampes centrum. 

For overskuelighedens skyld farvelægger vi nogle af stregerne: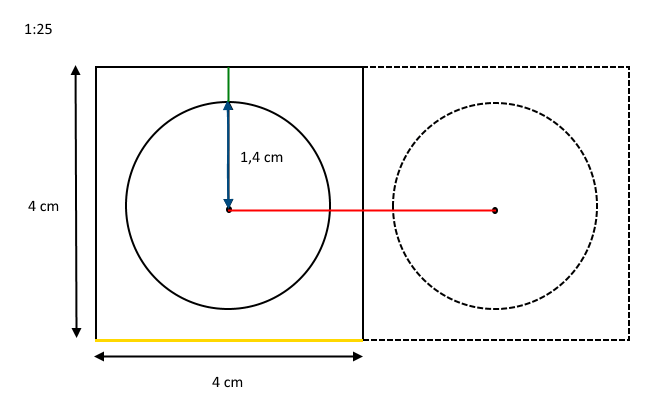

Da lamperne er ens, og skal placeres på samme måde, har de samme radius (blå linje). Ligeledes har lampernes kant samme afstand (grøn linje) hen til gipspladens kant. På tegningen kan vi derfor se, at hvis vi lægger radius for de to lampers (blå linje) sammen med lampernes afstand til gipspladens kant (grøn linje), så får vi afstanden mellem lampernes centrum (rød linje). Vi skal altså finde målene på lampernes radiusser og deres kanters afstand til gipspladens kant i virkeligheden. 

Vi starter med lampernes radius. Fordi vi skal finde målene i virkeligheden ud fra tegningen skal vi gange med 25. Altså:
Radius af lampe: \( 1,4 cm \cdot 25 = 35 cm \) 

Nu mangler vi bare at finde afstanden fra lampens kant til gipspladens kant (grøn linje). Hvis vi ser på tegningen, kan vi se hvis vi lægger længden af 2 blå linjer sammen med længden af 2 grønne linjer, får vi længden af gipspladens side (gul linje). Altså:

\( (2 \cdot \mathrm{blå} \ \mathrm{linje}) + (2 \cdot \mathrm{grøn} \ \mathrm{linje}) = \mathrm{gul} \ \mathrm{linje} \)
\((2 \cdot 1,4 cm) +  (2 \cdot \mathrm{grøn} \ \mathrm{linje}) = 4 cm \)
\(2 \cdot \mathrm{grøn} \ \mathrm{linje} = 4 cm - (2 \cdot 1,4 cm)  \)
\(\mathrm{grøn} \ \mathrm{linje} = \frac{4 cm - (2 \cdot 1,4 cm)}{2} \)
\(\mathrm{grøn} \ \mathrm{linje} = \frac{1,2 cm)}{2} = 0,6 cm \)

Da vi skal finde afstanden i virkeligheden ganger vi igen med 25. Altså:
Afstand fra lampekant til gipsplade kant: \( 0,6 cm \cdot 25 = 15 cm \)

Nu mangler vi bare at lægge tingene sammen.

\( \mathrm{afstand}  \ \mathrm{mellem} \ \mathrm{centrum} =(2 \cdot \mathrm{lampe} \ \mathrm{radius}) + (2 \cdot \mathrm{kantafstand}) \)
\( \mathrm{afstand}  \ \mathrm{mellem} \ \mathrm{centrum} = ( 2 \cdot 35 cm) + ( 2 \cdot 15 cm)  \)
\( \mathrm{afstand}  \ \mathrm{mellem} \ \mathrm{centrum} = 70 cm + 30 cm = 100 cm = 1 m \)

Hertil har vi brugt, at 1 m svarer til 100 cm. 

Altså skal lamperne placeres med en afstand på 1 m mellem deres centrum.  Hvis vi f.eks. skal borer et hul til en ledning i gipspladen, hvor lampens centrum er, skal vi altså bore huller med en afstand på 1 m mellem.