Materialeberegning, areal og rumfang
Uanset hvor stor en vej, der skal asfalteres - om det er en lokal villavej eller en stor motorvej - skal der anvendes asfalt. Men hvordan finder vi præcist ud af, hvor meget asfalt, der skal bruges til en bestemt vej?
Mængden af asfalt hænger sammen med vejens form, dens bredde og længde. Der skal ikke anvendes samme asfalt til en smal cykelsti, som til en stor motorvej. Men hvis mængden af asfalt hænger sammen med vejens form, er vi nødt til at kigge på emner som areal og rumfang for at finde ud af, hvor meget asfalt der skal anvendes.
Nedenfor gennemgår vi eksempler på, hvordan areal og rumfang anvendes til at beregne mængden af asfalt, der skal bruges til at asfaltere en vej. Skulle du undervejs blive i tvivl om, hvor formlerne kommer fra, kan du læse vores sider om areal og rumfang, hvor disse emner er beskrevet for en lang række kendte figurer. Inden eksemplerne gennemgår vi dog en række huskeregler.
Areal er et udtryk for hvor meget noget fylder på en flad overflade. Lejligheder og rum er f.eks. typisk angivet i m2. Gulv er f.eks. en flad overflade, og hvis vi har fået oplyst at en lejlighed er på 50 m2, betyder det altså at der er 50 m2 gulvplads.
Rumfang er til gengæld et udtryk for hvor meget noget kan indeholde. F.eks. indeholder en mælkekarton 1 liter mælk, eller en malerbøtte kan indeholde 5 liter maling.
Hvis vi skal finde ud af hvor meget asfalt, der skal anvendes til et bestem stykke vej med en specifik tykkelse, skal vi altså finde rumfanget. Skal vi derimod finde ud af, hvor stor en parkeringsplads er, skal vi finde arealet.
Det er dog ikke alle figurer, der er lige nemme at regne arealet eller rumfanget på. Og det er heller ikke alle former, vi har en formel for. Derfor er det vigtigt, når vi regner areal og rumfang ud, at vi inddeler en måske kompliceret figur i mindre figurer, som vi så kan regne areal eller rumfang på, og til sidst lægger vi det hele sammen, så vi får det samlede areal eller rumfang.
Nu er vi klar til eksemplerne.
Eksempler
1: Villavej
Ved en villavej skal der lægges ny asfalt. Vejen måler 400 m og er 5 m bred. Arbejderne skal lægge 65 kg asfalt pr. m2. Opgaven lyder på at finde ud af, hvor mange kg asfalt, der i alt skal lægges.
Vi kan betragte vejen som et rektangel med en side på 400 m og en anden side på 5 m. Ganger vi siderne sammen får vi det samlede areal af vejen:
$$ 400 m \cdot 5 m = 400 \cdot 5 m^2 = 2000 m^2 $$
Da der skal lægges 65 kg asfalt pr. m2, skal der i alt anvendes:
$$ 2000 m^2 \cdot 65 kg \ pr. \ m^2 = 130000 kg = 130 ton $$
Hertil har vi brugt at 1 ton svarer til 1000 kg.
2: Asfaltering af parkeringsplads
I forbindelse med en opførsel af et nyt supermarked, skal der asfalteres en ny parkeringsplads, der ser ud som vist på tegningen nedenfor.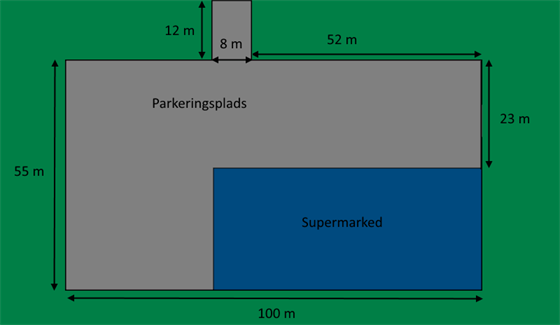 
I dette eksempel ser vi bort fra afmærkningen af parkeringsbåse. Asfalteringen skal være 3 cm tyk. Opgaven lyder på at finde ud af, hvor mange m3 parkeringsplads, der skal asfalteres.
Da parkeringspladsen ikke har en form, som vi direkte kan regne på, inddeler vi parkeringspladsen i en række rektangler.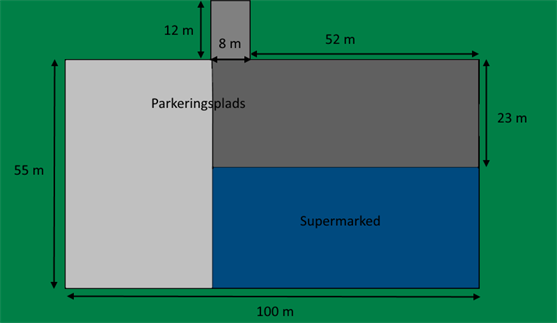
Hvert parkeringstykke der er inddelt, kan vi betrage som en kasse med en højde på 3 cm samt en bredde og en længde. Rumfanget af en kasse er givet som højde gange bredde gange længde. Vi skal nu blot finde længden og bredden af hver kasse, for at kunne finde rumfanget.
Rumfang af vejstykke:
Ud fra tegningen kan vi se at det lille vejstykke (mindste rektangel) er 8 m bredt og 12 m langt. Rumfanget bliver derfor:
$$ 3 cm \cdot 8 m \cdot 12 m = 0,03 m \cdot 8 m \cdot 12 m = 0,03 \cdot 8 \cdot 12 m^3 = 2,88 m^3 $$
Hertil har vi brugt at 1 m svarer til 100 cm.
Rumfang af mørkt rektangel:
På tegningen kan vi se, at et af rektanglens sider er 23 m. Hvis vi lægger 52 m til de 8 m, der udgør vejstykkets bredde, får vi længden af det mørke rektangels anden side. Rumfanget bliver derfor:
$$ 0,03 m \cdot 23 m \cdot (52 m + 8 m ) = 0,03 \cdot 23 \cdot 60 m^3 = 41,4 m^3 $$
Rumfang af lyst rektangel:
På tegningen kan vi se, at et af rektanglens sider er 55 m. Hvis vi trækker de 60 m, som udgør længden af det mørke rektangel, fra de 100 m, får vi præcis længden af det lyse rektangels anden side. Rumfanget bliver derfor:
$$ 0,03 m \cdot 55 m \cdot (100m -60 m) = 0,03 \cdot 55 \cdot 40 m^3 = 66 m^3 $$
Der skal altså i alt asfalteres:
$$ 2, 88 m^3 + 41, 4 m^3 + 66 m^3 = 110,28 m^3 $$