Pythagoras' læresætning og vinkelberegning
De fleste har nok hørt sin matematiklærer fortælle remsen "a i anden plus b i anden er lig med c i anden". Men hvad er det helt konkret, at remsen fortæller?
Remsen kaldes Pythagoras' læresætning, og den fortæller egentlig bare, hvordan der er en sammenhæng mellem sidelængderne i en retvinklet trekant. Pythagoras' læresætning udgør altså en opskrift på, hvordan vi finder længden af én side i en trekant, hvis vi kender længden af de to andre sider, og hvis vi ved, at trekanten er retvinklet (læs mere her).
Selvom trekanten ikke er retvinklet, kan vi faktisk benytte os af Pythagoras' læresætning. Enhver trekant kan nemlig inddeles i retvinklede trekanter ved hjælp af en hjælpelinje.
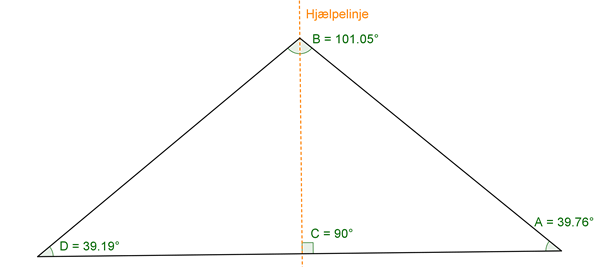
For at kunne regne på trekanter, skal man også vide noget om vinkler. Man skal fx vide, at hvis to linjer danner et kryds, så vil de to vinkler, der står over for hinanden, være lige store. Denne egenskab kan ses på tegningen nedenunder.

Her kan vi se, at vinkel A og vinkel B som står over for hinanden, begge er \(43^{\circ}\), mens vinkel C og vinkel D som står over for hinanden, er \(137^{\circ}\).
Denne viden omkring trekanter og vinkler er meget nyttig inden for tømrer-faget. Uanset om man skal bygge hele skelettet til et hus eller bare lægge et tag, kan man ikke undgå at støde ind i trekanter.
Nedenfor gennemgår vi nogle eksempler på, hvordan Pythagoras' læresætning og vinklernes egenskaber kan benyttes direkte i en tømrers job.
Eksempler
1: Tagkonstruktioner
For at lave et skråt tag på et hus, bygger man ofte nogle A-lignende konstruktioner, der skal være under taget for at støtte det. Disse konstruktioner kaldes for spær, og arbejdet med at bygge spærene udføres af en tømrer. I dette eksempel har en tømrer fået til opgave at bygge spærene til et hus med skråt tag. Tømreren har fået udleveret følgende tegning:
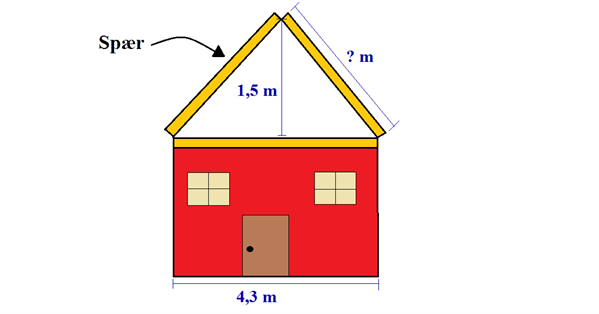
De gule træ-bjælker, der tilsammen udgør en trekant, er det omtalte spær. Tømreren ved altså, at huset er 4,3 meter bredt, samt at der fra husets loft til tagets spids skal være 1,5 meter. Han skal nu beregne, hvor lange de bjælker, der udgør den skrå del af spæret, skal være.
Fremgangsmåde:
Trekanten, der udgøres af spærets bjælker, er ikke nogen retvinklet trekant. Derfor bruger man den blå hjælpelinje, der angiver afstanden mellem husets loft og tagets spids. Den inddeler trekanten i to retvinklede trekanter, så det er muligt at bruge Pythagoras' læresætning til at løse opgaven. For helt præcist at se, hvordan Pythagoras' læresætning skal bruges på dette problem, skærer vi den ene af de to retvinklede trekanter ud, og navngiver dens sider med de velkendte \(a\), \(b\) og \(c\).
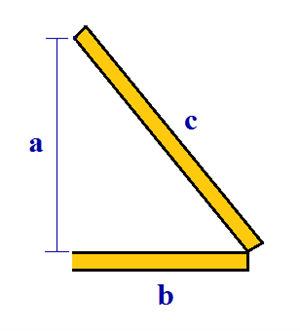
Hvis vi kan finde ud af, hvor lange \(a\) og \(b\) er, kan vi også udregne, hvor lang \(c\) er, og dermed hvor lang den skrå bjælke skal være. Fra tegningen af huset fremgår det, at \(a=1,5m\). Længden af \(b\) bliver faktisk også afsløret i tegningen af huset, idet den jo bare er halvdelen af bredden af huset. Altså er
$$b=\frac{4,3m}{2}=2,15m.$$
Ifølge Pythagoras' læresætning gælder der at
$$a^2+b^2=c^2.$$
Hvis vi erstatter \(a\) og \(b\) med de tal vi har beregnet dem til, får vi følgende udtryk:
$$(1,5)^2+(2,15)^2=c^2.$$
Dette er en ligning, som vi nu kan løse ud fra fremgangsmåden beskrevet i afsnittet om ligninger. Det eneste vi lige skal være opmærksomme på her, er at den ubekendte i dette tilfælde hedder \(c\), og ikke \(x\) som vi ellers er vandt til. For at finde den værdi af \(c\) der løser ligningen, skal vi have fjernet det \(2\)-tal, som \(c\)'et er opløftet i. Dette gøres ved at anvende den "modsatte" funktion på begge sider af lighedstegnet. Den modsatte funktion af "opløftet i 2.", er kvadratroden. Dermed får vi at
$$\sqrt{(1,5)^2+(2,15)^2}=\sqrt{c^2}.$$
Nu kan vi se, at kvadratroden og 2-tallet som \(c\) er opløftet i, går ud med hinanden på højre side af lighedstegnet. Tilbage har vi så
$$\sqrt{(1,5)^2+(2,15)^2}=c.$$
Vi kan regne ud hvad venstre-siden af lighedstegnet er, ved fx at bruge en lommeregner. Ligningens venstre-side giver
$$\sqrt{(1,5)^2+(2,15)^2}=2,62.$$
Derfor er
$$c=2,62.$$
Det vil sige, at hvis huset er 4,3 meter bredt, og der skal være 1,5 meter fra husets loft til tagets spids, så skal de bjælker, der udgør den skrå del af spæret, være 2,62 meter lange hver.
2: Vinkelberegning
En tømrer bliver sat til at skulle bygge rammen til et indgangsparti til en have. Rammen skal laves i træ, og den færdige ramme skal se ud som på billedet herunder.
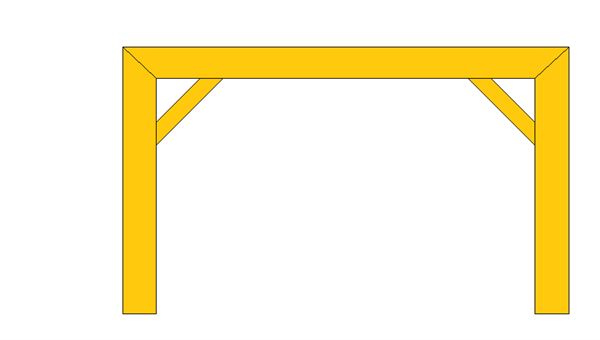
Tømren ønsker nu at finde ud af, hvordan han finder den rigtige vinkel, som de skrå støttebrædder i hjørnerne, skal saves med.
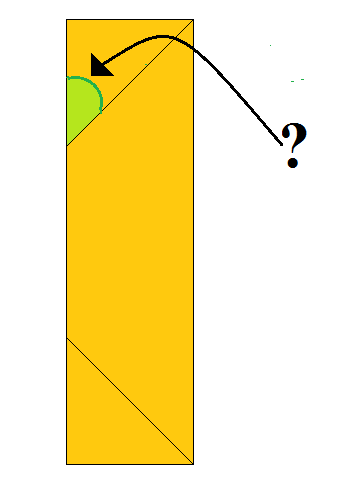
Fremgangsmåde:
Tømren skal nu bruge sin viden om vinkler i en trekant, for at beregne den rigtige vinkel at save bræddet i. Hvis vi zoomer lidt ind på hjørnet af konstruktionen, kan vi få et nærmere indblik i, hvilken konkret trekant, der er i spil.
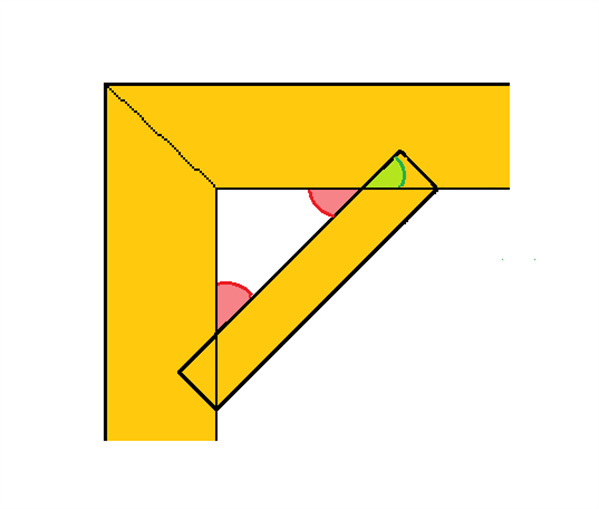
Det er blevet oplyst, at det skrå brædde skal sidde således, at de to røde vinkler, er ens. Denne oplysning er nyttig for tømren, når han skal beregne den grønne vinkel. Først skal vi have beregnet den røde vinkel. Til dette kan vi benytte vores viden om vinkler i en trekant fra afsnittet om trekanter. Der skal nemlig gælde at summen af de tre vinkler i en trekant, skal være \(180^{\circ}\). I den trekant der indeholder de to røde vinkler, er den tredje vinkel en ret vinkel, dvs. en vinkel på \(90^{\circ}\). Da summen af vinklerne skal give \(180^{\circ}\), skal de to røde vinkler tilsammen udgøre
$$180^{\circ}- 90^{\circ}= 90^{\circ}.$$
Eftersom de to røde vinkler skulle være lige store, skal de altså hver være
$$\frac{90^{\circ}}{2}=45^{\circ}.$$
Vi kan nu beregne den grønne vinkel, som er den vinkel, tømren ønsker at finde. Dette kan gøres ved at benytte, at når to linjer danner et kryds, så er de to vinkler der står over for hinanden lige store. Da vi lige har beregnet den røde vinkel til at være \(45^{\circ}\), må den grønne vinkel derfor ligeledes være \(45^{\circ}\). Det vil sige, at tømren skal save brættet med en vinkel på \(45^{\circ}\).
3: En rigtig byggeplads
I videoen nedenfor kan du se hvordan Daniel, tømrersvend hos NCC, benytter Pythagoras læresætning i sin hverdag.
