Blandede forbindelser
Blandede forbindelser
Blandede forbindelser er elektriske kredsløb, hvor komponenterne både sidder i serie og i parallel. Et eksempel kan ses nedenfor,
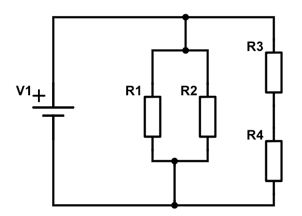
Kredsløbet har tre modstande, hvor der både indgår serie- og parallelforbindelser. Hvordan finder man kredsløbets totale modstand?
Man er nødt til at inddele kredsløbet i mindre dele, for at finde den totale modstand. Først ser vi på \( R_1 \) og \( R_2 \).De to modstande sidder i parallel med hinanden. Derfor kan man finde den totale resistens for kun de to komponenter, som vi kalder \( R_{12} \). Vi får derfor
$$ (R_1^{-1}+R_2^{-1})^{-1} = R_{12} $$
Kredsløbet kan nu tegnes som
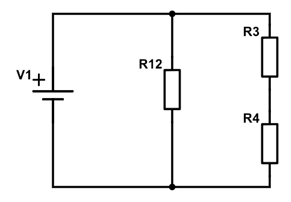
Nu har vi to modstande i serie, hvor vi simpelt kan lægge dem til hinanden, for at finde den totale resistans.
$$ R_3+R_4 = R_{34} $$
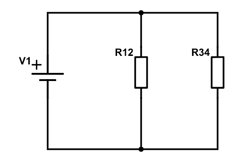
Nu har vi endnu en gang to modstande i parallel. De kan samles og hermed findes den totale modstand for kredsløbet,
$$ (R_{12}^{-1}+R_{34}^{-1})^{-1} = R_{1234}$$
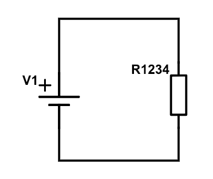
Eksempel 1
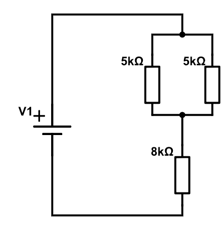
Vi ønsker at finde den samlede modstand i kredsløbet. Vi gør som ovenfor, og finder den totale modstand for de to \(5k\Omega\) modstande.
$$ \frac{1}{5k\Omega}+\frac{1}{5k\Omega} = \left( \frac{2}{5k\Omega} \right)^{-1} = 2.5k\Omega $$
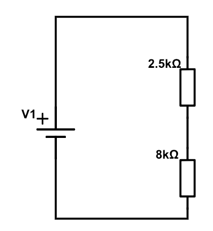
Eftersom modstandene nu sidder i serie, kan vi simpelt lægge dem til hinanden
$$ 2.5k\Omega + 8k\Omega = 10.5k\Omega $$
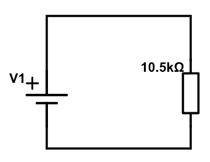
En typisk opgave: Udfyld tabellen
En typisk opgave man kan blive stillet inden for blandede forbindelser inkluderer to elementer: et kredsløbsdiagram og en tabel, hvor der mangler værdier. For at løse opgaven skal man udfylde tabellen. Det kan kun gøres, hvis man er i stand til at regne med parallel- og serieforbindelser samt at man har tjek på Ohms lov.
Vi har derfor givet følgende kredsløb:
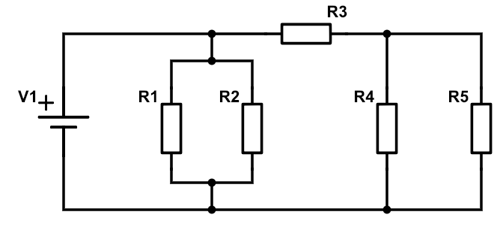
Vi får følgende oplyst:
| Komponent | R1 | R2 | R3 | R4 | R5 | Total |
| Spænding (V) | ||||||
| Strøm (A) | \(10A\) | |||||
| Modstand (\( \Omega\)) | \(10\Omega\) | \(30\Omega\) | \(15\Omega\) | \(12\Omega\) | \(12\Omega\) |
Vi kender størrelsen på alle modstande i kredsløbet. Derfor starter vi med at bestemme den totale modstand i kredsløbet.
Vi starter med at samle R4 og R5, som sidder parallelt med hinanden, til R45 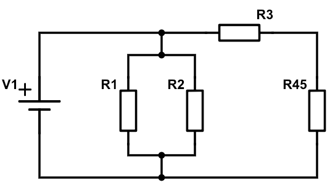
$$ R45 = \left(12\Omega^{-1}+12\Omega^{-1}\right)^{-1} = 6\Omega$$
Nu kan R3 og R45 samles, da de sidder i serie, til R345,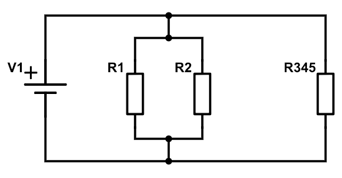
$$ R345 = 15\Omega+6\Omega = 21\Omega$$
Næste trin er at samle R1 og R2, som sidder i parallel, til R12,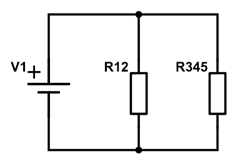
$$ R12 = \left(10\Omega^{-1}+30\Omega^{-1} \right)^{-1} = 7{,}5\Omega$$
Til sidst samler vi R12 og R345, og finder dermed den totale modstand i kredsløbet, R_TOTAL,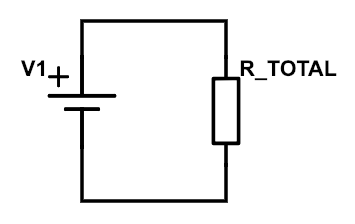
$$ R\_TOTAL = \left(7{,}5\Omega^{-1}+21\Omega^{-1}\right)^{-1} = 5{,}53\Omega$$
Vi kan nu udfylde et par felter i tabellen, da vi kender kredsløbets totale modstand. Da vi kender den totale strøm i kredsløbet, kan vi udregne den totale spænding i kredsløbet, ved hjælp af Ohms lov (\(U=R\cdot I\)):
$$ 10A \cdot 5{,}53\Omega = 55{,}3V $$
| Komponent | R1 | R2 | R3 | R4 | R5 | Total |
| Spænding (V) | \(55{,}3V\) | |||||
| Strøm (A) | \(10A\) | |||||
| Modstand (\( \Omega \)) | \( 10\Omega\) | \(30\Omega \) | \(15 \Omega\) | \(12 \Omega\) | \( 12\Omega\) | \( 5{,}53\Omega\) |
Nu kan vi begynde at fylde værdier ind i de tomme felter. Hvis vi ser på det samlede kredsløb, kan vi se, at R1 og R2, som er parallelle, sidder i parallel med de resterende tre komponenter. Da spændingsfaldet over parallelle komponenter er ens, må spændingsfaldet over R1 og R2 være lig med spændingsfaldet over R3, R4 og R5. Vi kan også se, at spændingsfaldet over R1 og R2 tilsammen må være lige det samlede spændingsfald i kredsløbet, altså \(55{,}3V\). Nu da vi kender spændingsfaldet, kan vi bestemme strømmen, som bliver afsat i R1 og R2.
$$ R1_A = \frac{55{,}3V}{10\Omega} = 5{,}53A \\ R2_A = \frac{55{,}3V}{30\Omega} = 1{,}84A $$
Nu kender vi den samlede strøm, som afsættes i R1 og R2, nemlig \( 7{,}37A\). Det betyder, at den strøm som afsættes i R3, R4 og R5 tilsammen må være \(2{,}63A\). Vi ved at strømmen gennem komponenter i serie er ens, derfor må strømmen gennem R3 være lig med strømmen gennem R4 og R5, tilsammen. Derfor kan vi bestemme spændingen over R3, da vi nu kender både modstand og strøm,
$$ R3_A = 2{,}63A \cdot 15\Omega = 39{,}5V$$
Da vi nu har bestemt spændingen i R3, kan vi finde spændingen over R4 og R5:
$$ R(4+5)_V = 55{,}3V-39{,}5V = 15{,}8V $$
Vi kan nu bestemme strømmen gennem R4 og R5, da vi kender to ud af tre værdier,
$$ R4_A = \frac{15{,}8V}{12\Omega} = 1{,}32A$$
$$ R5_A = \frac{15{,}8V}{12\Omega} = 1{,}32A$$
Strømmen gennem R4 og R5 er derfor \(1,32A\) +\(1,32A\) = \(2,64A\), hvilket er lig med strømmen gennem R3 (differencen på 0,01 A skyldes blot afrunding).
Vi kan nu udfylde vores skema:
| Komponent | R1 | R2 | R3 | R4 | R5 | Total |
| Spænding (V) | \(55{,}3V\) | \(55{,}3V\) | \(39{,}5V\) | \(15{,}8V\) | \(15{,}8V\) | \(55{,}3V\) |
| Strøm (A) | \(5{,}53A\) | \(1{,}84A\) | \(2{,}63A\) | \(1{,}32A\) | \(1{,}32A\) | \(10A\) |
| Modstand (\( \Omega \)) | \( 10\Omega\) | \(30\Omega \) | \(15 \Omega\) | \(12 \Omega\) | \( 12\Omega\) | \( 5{,}53\Omega\) |
