Parallelforbindelser
Parallelle forbindelser
Parallelle forbindelser kan ses på figuren nedenfor.
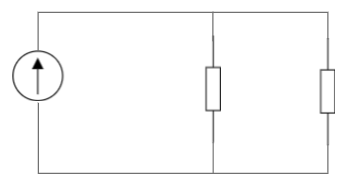
Her sidder de to modstande "over for" hinanden. Strømmen i kredsløbet er nødt til at dele sig, så den løber igennem begge modstande på samme tid. I sådan et kredsløb, findes erstatningsmodstanden som
$$ \left( \frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+...\right)^{-1} = R_{tot}$$
Omvendt af serieforbindelser, så ændrer spænding sig ikke over to komponenter i parallel. Dette er grunden til, at et voltmeter skal sidde i parallel med den komponent man ønsker at bestemme spændingen over.
Strømmen derimod, den falder, fordi der sker en strømdeling, hver gang kredsløbet deler sig.
HUSKEREGEL: Hvis to modstande sidder i parallel og har samme værdi, vil erstatningsmodstanden af de to modstande være halvt så stor, som én af dem, f.eks. \( \left( \frac{1}{10k\Omega}+\frac{1}{10k\Omega} \right)^{-1} = 5k\Omega\).