Materialeberegning: areal og rumfang

Uanset hvilket byggeprojekt der arbejdes på - om der skal graves tunneler, støbes beton eller bygges broer - skal der anvendes materialer. Et naturligt spørgsmål er derfor: Hvor stor en mængde materialer, skal der anvendes?

Mængden af materialer hænger sammen med, hvordan de skal anvendes, og dermed hvilken form, de skal anvendes til. Det er ikke det samme at skulle støbe en betoncylinder, som det er at bygge en bro. Derfor er vi nødt til at kigge på areal og rumfang af de forme, der skal bygges, for at finde ud af, hvor meget materiale der skal anvendes. 

Nedenfor gennemgår vi eksempler på, hvordan areal og rumfang anvendes ved byggeprojekter til at beregne mængden af materialer. Skulle du undervejs blive i tvivl om, hvor formlerne kommer fra, kan du læse vores sider om areal og rumfang, hvor disse emner er beskrevet for en lang række kendte figurer. Inden eksemplerne gennemgår vi dog en række huskeregler.

Areal er et udtryk for hvor meget noget fylder på en flad overflade. Lejligheder og rum er f.eks. typisk angivet i m². Gulv er f.eks. en flad overflade, og hvis vi har fået oplyst at en lejlighed er på 50 m², betyder det altså at der er 50 m² gulvplads. 
Rumfang er til gengæld et udtryk for hvor meget noget kan indeholde. F.eks. indeholder en mælkekarton 1 liter mælk, eller en malerbøtte kan indeholde 5 liter maling.

Hvis vi skal finde ud af hvor meget beton en betonklods indeholder, skal vi altså finde rumfanget. Skal vi derimod finde ud af, hvor meget et betongulv fylder, skal vi finde arealet.

Det er dog ikke alle figurer, der er lige nemme at regne arealet eller rumfanget på. Og det er heller ikke alle former, vi har en formel for. Derfor er det vigtigt, når vi regner areal og rumfang ud, at vi inddeler en måske kompliceret figur i mindre figurer, som vi så kan regne areal eller rumfang på, og til sidst lægger vi det hele sammen, så vi får det samlede areal eller rumfang.

Nu er vi klar til eksemplerne.

Eksempler

1: Betongulv

Vi har fået opgivet følgende tegning af et betongulv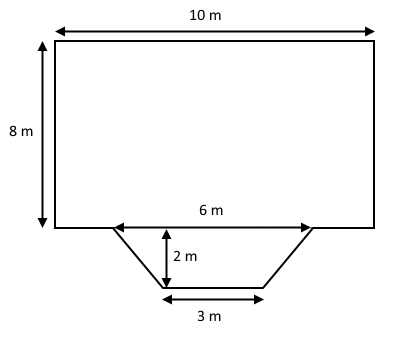
Betongulvet skal overfladebehandles, og der anvendes 1 liter af materialet til overfladebehandling pr. 7 m². Opgaven lyder på at finde ud af hvor mange liter af materialet, der skal anvendes. 

Da gulvet er en flad overflade skal vi altså finde arealet, for at kunne finde ud af, hvor mange liter vi skal bruge. Gulvet har i sin helhed ikke en form som en figur, som vi direkte kan regne på. Vi opdeler derfor figuren i to mindre dele - en rektangel og en trapez.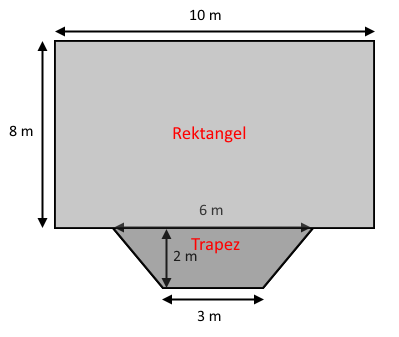 
Vi regner nu arealet af hver af de to figurer, og lægger arelaet sammen bagefter.

Areal af rektangel:
Arealet af en rektangel er givet som; længden af den ene side gange længden af den anden side. Vi får derfor:
$$ 8 m \cdot 10 m = 8 \cdot 10 m^2 = 80 m^2 $$

Areal af trapez:
Arealet af en trapez er givet som; summen af længden af de to parallele sider gange halvdelen af højden. Vi får derfor:
$$ \frac{1}{2}\cdot 2m \cdot (6 m+3m) =  \frac{1}{2}\cdot 2m \cdot 9m =  \frac{1}{2}\cdot 2 \cdot 9 m^2 = 9 m ^2 $$

Det samlede areal bliver derfor:
$$ \mathrm{areal} \  \mathrm{af} \ \mathrm{rektangel} + \mathrm{areal} \ \ \mathrm{af} \  \mathrm{trapez} = 80 m^2 + 9 m^2 = 89 m^2 $$

Vi har altså 89 m² betongulv.  Da 7 m² af gulvet kan dækkes pr. liter, skal vi i alt bruge: 
$$ \frac{89 m^2}{7 m^2 \ pr. \ liter} = 12, 71 \ liter $$
Vi skal altså bruge 12,71 liter af overfladebehandlingen. 

2: Rumfang af betonrør

 I forbindelse med et byggeprojekt, skal der støbes følgende betonrør.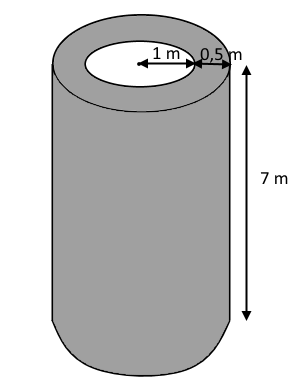
Betonet der anvendes har en massefylde på 2,3 ton pr. m³. Opgaven lyder på finde ud af, hvor mange ton beton, der skal anvendes til røret. 

Da vi skal finde ud af, hvor meget beton røret består af - dvs. hvor meget beton røret indeholder - skal vi altså finde rumfanget. Igen har røret ikke en form, som vi har en direkte formel på. Men hvis vi ser på tegningen kan vi se at hulrummet i røret udgør en cylinder. Samtidig udgør hulrummet og betonrøret tilsammen en endnu større cylinder. Hvis vi trækker rumfanget af hulrummet fra rumfanget af den store cylinder, får vi præcis rumfanget af betonrøret. Vi skal derfor først finde rumfanget af den store cylinder og hulrummet. 

For en cylinder er rumfanget givet som:
$$ \mathrm{rumfang}_{cylinder} = h \cdot \pi \cdot r^2 $$
Hvor h er højden og r er radius af cirkeltoppen. 

Rumfang af stor cylinder:
Hvis vi ser på tegningen er radius af den store cylinder givet som radius af hulrummet plus tykkelsen af røret. Højden er den samme som højden af betonrøret. Rumfanget af den store cylinder bliver derfor:
$$ 7 m \cdot \pi \cdot (1 m + 0,5m)^2= 7m \cdot \pi \cdot (1,5 m)^2 = 7 m \cdot \pi \cdot 2,25 m^2 = 7 \cdot 2,25 \cdot \pi m^3 = 49,48 m^3 $$

Rumfang af hulrum:
Ud fra tegningen kan vi se, at radius af hulrummet er 1 m. Højden er den samme som højden af betonrøret. Rumfanget af hulrummet bliver derfor:
$$ 7 m \cdot \pi \cdot (1 m)^2 = 7 m \cdot \pi \cdot 1 m^2 = 7\cdot \pi m^3 = 21,99 m^3 $$

Rumfanget af betonrøret bliver derfor:
$$ \mathrm{rumfang}_{stor \ cylinder} - \mathrm{rumfang}_{hulrum} = 49,48 m^3 - 21,99 m^3 = 27,49 m^3 $$

Røret består altså af 27,49 m³ beton. Den anvendte mængde af beton i ton bliver derfor:
$$ 27,49 m^3 \cdot 2,3 \ ton \ pr. \ m^3 = 63, 23 \ ton $$

Der skal altså anvendes 63,23 ton beton.