Cirkler

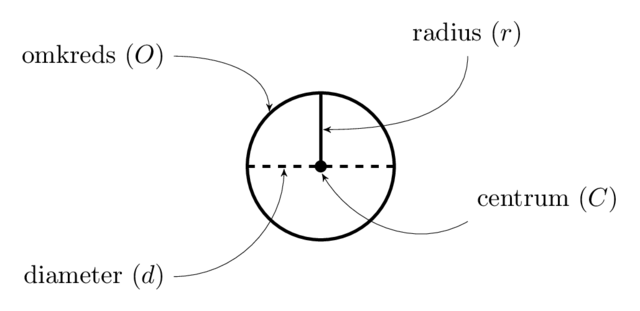
Cirkler kan nemt tegnes med en passer, og den streg, som passeren tegner, kaldes for cirklens omkreds. Alle cirkler har desuden et centrum og alle punkter på omkredsen (også kaldet cirkelperiferien) ligger lige langt væk fra centrum. Denne strækning kaldes for cirklens radius og 2 radier danner en diameter (se billedet nedenunder).

Når man snakker cirkler snakker man også rigtig tit om korder og tangenter. En korde er en ret linje som forbinder to punkter der ligger på omkredsen (periferien). Et specialtilfælde af en korde er diameteren. Her går korden igennem centrum. 
En tangent derimod er en ret linje som kun har ét berøringspunkt med cirklen (se evt. billedet nedenunder). 

Omkredsen af en cirkel er givet ved

$$
\begin{array}{rcl}
\mathrm{omkreds} & = & \pi \cdot \mathrm{diameter} \\
O & = & \pi \cdot d.
\end{array}
$$

Altså skal vi kende diameteren for at kunne regne omkredsen af en cirkel. Vi ved dog også at \(d=2\cdot r\) og således kan vi også bestemme omkredsen ud fra cirklens radius

$$
O = 2\pi \cdot r.
$$

Cirkeludsnit

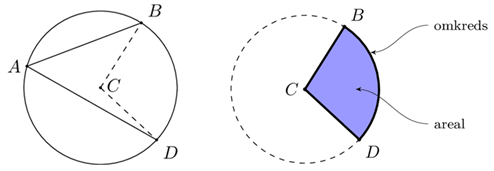
Hvis vi kigger på ciklen th. nedenunder kan vi se at omkredsen af cirkeludsnittet er summen af to radier og den bue, som ligger på cirklens omkreds. For at regne længden af buen er vi nødt til at se hvor lang buestykket er i forhold til cirklens omkreds, hvilket vi skal bruge centervinklen (se cirklen tv.) \(\angle BCD\) til. 

Hvis vi betegner vores centervinkel som \(\phi\) (det græske bogstav phi, udtales fi) så vil omkredsen af cirkeludsnittet være givet ved

$$
O_{udsnit} = \frac{\pi r}{180^{\circ}}\cdot\phi + 2r.
$$

 

 

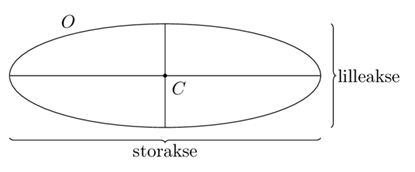
Ellipser

En ellipse er, på sin vis, en cirkel der er blevet strukket ud til siderne. Dette gør dog sådan at der ikke længere er den samme afstand fra centrum og ud til alle punkter på omkredsen. I stedet for at snakke om radius og diameter som vi gjorde for cirkler, så snakker vi om en stor- og lilleakse.