Statistik

Statistik

Statistik kan bruges til at beskrive en talmængde. Hver enkelt tal i en talmængde kaldes en observation. Antallet af observationer i talmængden, kaldes for talmængdens størrelse og bliver ofte skrevet som \(n\).

For eksempel vil vi lave statistik over karaktererne ved en eksamen. Der er 25 elever i klassen og der er givet følgende karakterer.

10     7    10    4    10     4     2    10     7     7    12     7     4     4     4    12     7    10     4    12     2     7     4     7     7

Da der er 25 elever i klassen er størrelsen

$$n = 25$$

Hyppighed

Hyppigheden af et tal fortæller hvor mange gange et tal optræder i en række af observationer.

I eksemplet med karaktererne kan hyppigheden af hver karakter skrives sådan her

Karakter	-3	00	02	4	7	10	12
Hyppighed \(h(x)\)	0	0	2	7	8	5	3

Hyppigheden kan også tegnes med et pindediagram

Frekvens

Frekvensen fortæller hvor stor en andel hyppigheden af et tal udgør af den samlede mængde.

$$\mathrm{frekvens} = \frac{\mathrm{hyppighed}}{\mathrm{størrelse}}$$

Dette kan også skrives simplere

$$f(x) = \frac{h(x)}{n}$$

Vi vil nu beregne frekvensen af hver karakter i eksemplet

For karakteren 02 er frekvensen

$$f(x)=\frac{h(x)}{n}=\frac{2}{25}=0,08 = 8\%$$

Karakter	-3	00	02	4	7	10	12
Frekvens \(f(x)\)	0	0	0,08	0,28	0,32	0,20	0,12

Summen af alle frekvenserne skal være lig med 1

$$0,08 + 0,28 + 0,32 + 0,20 + 0,12 = 1$$

Diagrammer

Der er flere måder af illustrere frekvensen på, her er nogle eksempler.

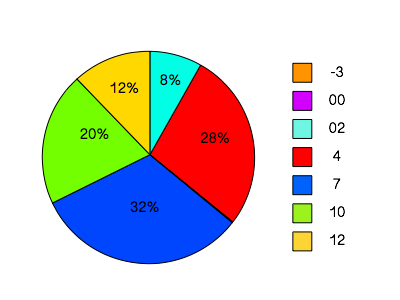
Cirkeldiagram

Et cirkel diagram består af en cirkel. Dele af cirklen er farvet eller skraveret alt efter frekvensen.

Her ses et eksempel på et cirkeldiagram over karakterene. Hver farve viser de forskellige karakterer og størrelsen af stykkerne viser frekvensen.

Kvadratdiagram

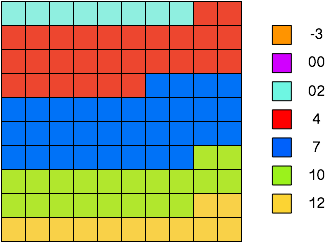
Et kvadratdiagram består af et kvadrat der er helt op i mindre kvadrater.

I dette eksempel på et kvadratdiagram er det store kvadrat delt op i 100 mindre kvadrater. Så der er 10 på hver led og et enkelt farvet kvadrat svarer til 1% af alle observationerne.

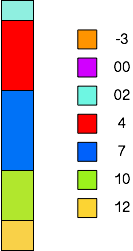
Stabeldiagram

Et stabeldiagram er meget ligesom et kvadrat diagram bortset fra at alle kvadraterne er stablet oven på hinanden for at danne en enkelt søjle.

Typetal

Typetallet er det tal der oftest forekommer i en række af observationer.

I eksemplet med karakterene er det den karakter som flest af eleverne har fået og altså 7.

Middelværdi

Middelværdien, eller gennemsnittet, af en række tal, beregnes ved at lægge alle tallene sammen og dividere med antallet af tal.

$$\bar{x} =  \frac{x_1 + x_2 + \dots + x_n}{n} =\frac{1}{n}\sum_i^n x_i$$

Middelværdi af karakterene i eksemplet ovenfor kan regnes ud sådan her

$$\bar{x} = \frac{2\cdot 2 + 7 \cdot 4 + 8 \cdot 7 + 5\cdot 10 + 3\cdot 12}{25} = 6.96$$

Medianen

Medianen angiver den midterste værdi i en talrække der er sorteret efter størrelsen. Det betyder at halvdelen af observationerne vil være større end medianen og halvdelen af observationerne vil være mindre end medianen.

Hvis der er et lige antal observationer er medianen gennemsnittet af de to midterste tal.

For eksempel, hvis vi sorterer alle elevernes karakterer fra laveste til højeste ser det sådan her ud

02, 02, 4, 4, 4, 4, 4, 4, 4, 7, 7, 7, 7, 7, 7, 7, 7, 10, 10, 10, 10, 10, 12, 12, 12

Er medianen det 13. tal i rækken som er 7.

Mindsteværdi og størsteværdi

Mindsteværdien er den mindste observation i rækken af observationer. I eksemplet med karaktererne ovenfor, er 02 mindsteværdien.

Størsteværdien er tilsvarende den største observation. Det vil altså være 12 i eksemplet ovenfor. 

Variationsbredde

Variationsbredden er forskellen mellem størsteværdien og mindsteværdien i rækken af observationer. Hvis vi fortsætter med eksemplet med karaktererne, så er variationsbredden:

$$ 12-2=10. $$

Vi får altså en variationsbredde på 10.