Trapez

Et trapez er en firkant, hvor to af siderne er parallelle. De parallelle sider kalder vi \(a_1\) og \(a_2\). De øvrige sider kunne man have kaldt \(b\) og \(c\), men de er ligegyldige, når vi skal finde arealet.

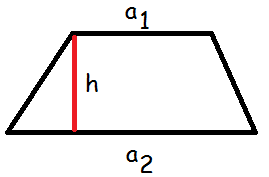
Arealet af et trapez er givet ved formlen:

$$A=\frac{1}{2}\cdot h\cdot (a_1+a_2)$$

Man lægger altså de to parallelle sider sammen, ganger med højden og dividerer med to.

Lad os nu se, hvorfor den formel ser ud som den gør.

Vi kan inddele trapezet i to trekanter.

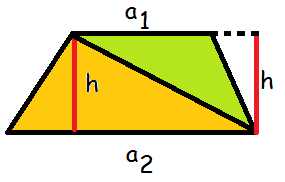
Den orange trekant har grundlinje \(a_2\) og højde \(h\), mens den grønne har grundlinje \(a_1\) og højde \(h\). Altså er deres arealer

$$T_{\mathrm{grøn}}=\frac{1}{2}\cdot h\cdot a_1$$

$$T_{\mathrm{orange}}=\frac{1}{2}\cdot h\cdot a_2$$

Trapezets areal må være summen af de to trekanters areal.

$$A_{\mathrm{trapez}}=\frac{1}{2}\cdot h\cdot a_1+\frac{1}{2}\cdot h\cdot a_2$$

Nu sætter vi \(\tfrac{1}{2}h\) udenfor parentes.

$$A_{\mathrm{trapez}}=\frac{1}{2}\cdot h\cdot (a_1+a_2)$$

Og sådan nåede vi frem til den formel.