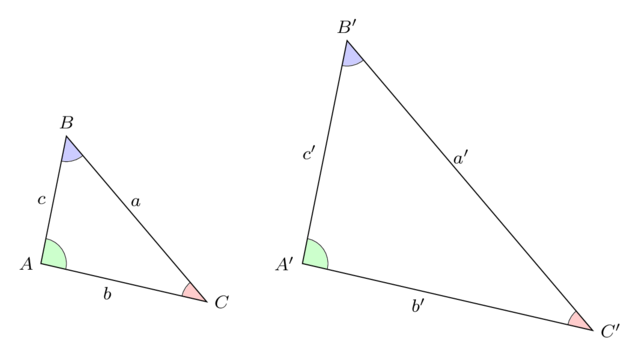
Ensvinklede trekanter

Ensvinklede trekanter kaldes også ligedannede trekanter. Det at to trekanter er ensvinklede betyder at der findes en skaleringsfaktor der kan "transformere" den ene trekant om til den anden. Denne skaleringsfaktor, også kaldet længdeforholdet, er ens for alle tre sider.

Hvis vi har to trekanter $\triangle ABC$ og $\triangle A' B' C'$ (se figuren nedenfor) og vi ønsker at finde ud af, hvor mange gange større den store trekant er i forhold til den lille, så tager vi blot forholdet mellem en af siderne i den store trekant og den tilhørende side i den lille trekant

$$k_{stor} = \frac{a'}{a} = \frac{b'}{b} = \frac{c'}{c}.$$

Ønsker vi derimod at finde ud af hvor mange gange mindre den lille trekant er i forhold til den store så tager vi bare det omvendte forhold

$$k_{lille} = \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'}.$$

Der skal desuden gælde at

$$k_{lille}\cdot k_{stor}=1.$$

Dette ses let hvis vi vælger $k_{lille}=\frac{a}{a'}$ samt $k_{stor}=\frac{a'}{a}$ for så får vi

$$k_{lille}\cdot k_{stor} = \frac{a}{a'}\cdot\frac{a'}{a} = 1.$$