Eksempler på lineære funktioner

Eksempel 1

Du er i slikbutikken for at blande slik. Prisen er 8 kr. pr. 100 gram.

Vi lader \(x\) betegne vægten af slik, du køber (målt i 100 g).

Vi lader \(y\) betegne prisen, du skal betale (målt i kr.).

Vi kan starte med at lave et sildeben over værdierne ved at se hvad prisen (\(y\)) bliver for forskellige mængder slik (\(x\)). Vi husker at hvis vi køber 300 g, så er \(x=3\), hvis vi køber 200 g er \(x=2\) osv.

x (mængde slik målt i 100 g)	y (pris i kr.)
1	8
2	16
3	24
4	32

Ud fra sildebenet kan vi tegne grafen

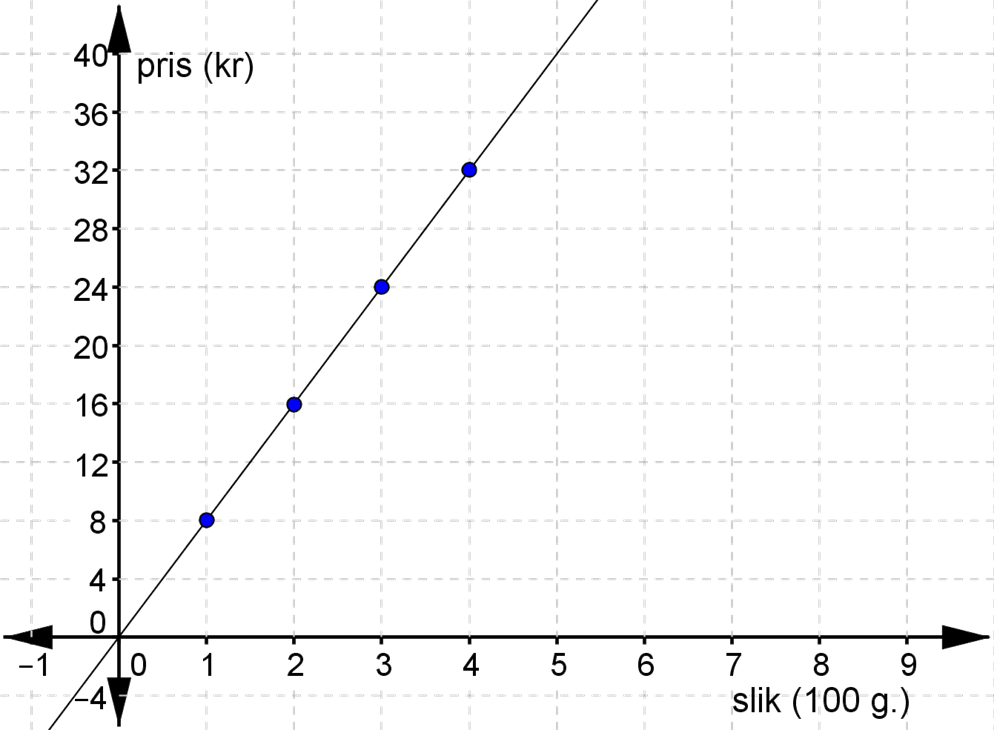
Ud fra grafen kan vi aflæse \(a\) (ved at gå 1 hen ad \(x\)-aksen og se, hvor meget grafen stiger).

Vi ser, at \(a=8\).

Vi ser, at grafen skærer \(y\)-aksen i punktet 0, så \(b=0\).

En forskrift for grafen er derfor

$$y=8\cdot x+0,$$

eller bare

$$y=8\cdot x.$$

Eksempel 2

Du er ude at køre taxa.

Det koster 50 kr. i startgebyr og 16 kr. pr. km.

Vi lader \(x\) være antal km. vi kører, og vi lader \(y\) være prisen for turen.

Hvis vi kører en km., så er prisen 50+16=66 kr.

Hvis vi kører 2 km. er prisen 50+16+16=82 kr.

Vi prøver med nogle flere værdier og laver et sildeben

x (antal kørte km.)	y (pris i kr.)
1	66
2	82
3	98
4	114

Vi prøver at opkrive en forskrift uden at tegne grafen for funktionen.

Vi kan se, at hver gang vi kører 1 km ekstra, så stiger prisen med 16kr.

Dermed er \(a=16\)

Vi kan se, at hvis vi bare satte os inde i taxaen uden at køre, så ville prisen være 50 kr.

Dermed er \(b=50\).

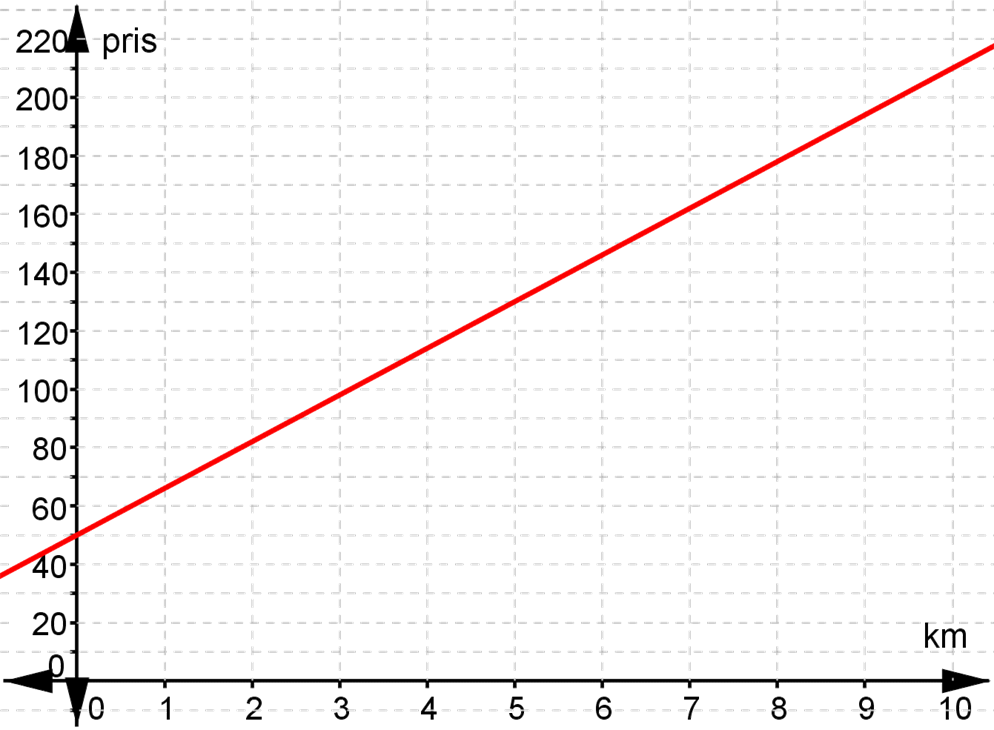
Sammenhængen er dermed

$$y=16\cdot x+50$$

Grafen ser sådan her ud