Isometrisk tegning

I dette afsnit beskrives arbejdstegning og isometrisk tegning. Indledningsvis kan der skelnes mellem arbejdstegningen som viser problemstilling fra kun én side, og den isometriske tegning som viser både højde, bredde og længde:

	Beskrivelse
Arbejdstegning	Tegning set fra én side med \(x\)- og \(y\)-akse
Ikke-parallel linje	Afstand skal beregnes - kan ikke aflæses
Isometrisk tegning	Tegning med samme enhed på \(x\)-, \(y\)- og \(z\)-akse
Målestoksforhold	Angiver størrelse enheden skal multipliceres med
Parallel linje	Isometrisk linje hvor distance kan aflæses direkte

Isometrisk linje

Så fremt en linje på den isometriske tegning er parallel med en af akserne, kaldes den for en isometrisk linje. Isometriske linjer kan måles direkte på tegningen imens øvrige linjer må beregnes med Pythagoras sætning (se evt. afsnittet om retvinklede trekanter).

Eksempel

Vi gør brug af både direkte aflæsning og beregning med pythagoras, ved at tage udgangspunkt i et eksempel:

Vi er netop flyttet ind i et hus med fladt tag. I stedet for fladt tag vil vi nu have bygget skråt tag med vinduer til at hente dagslys hvor tagets sider mødes. Længde, bredde og højde fra tagets top på huset før og efter ombygning er følgende:

	Før	Efter
Længde	15	15
Bredde	8	8
Højde af huset	5,5	7,5

Det er derfor kun højden der ændres i dette tilfælde. Yderligere har vi bestemt at toppen af taget skal sidde 5 m fra venstre (som set på tegningen).  For at illustrere dette laver vi først en arbejdstegning:

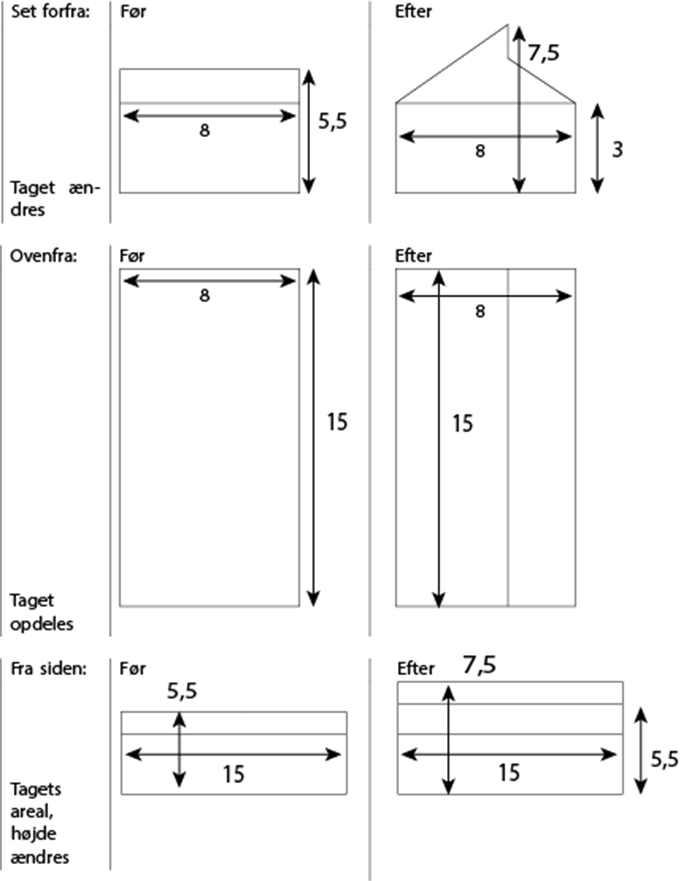
På baggrund af arbejdstegningerne kan vi udarbejde en isometrisk tegning, og via denne få visualiseret hvordan huset og ikke mindst taget vil blive efter ombygningen. I forbindelse med dette kan vi også beregne tagets nye vinkler og længden af de nye skrå tagflader som er ikke-parallelle. 

Først laver vi en lidt mere detaljeret arbejdstegning af huset forfra efter ombygningen

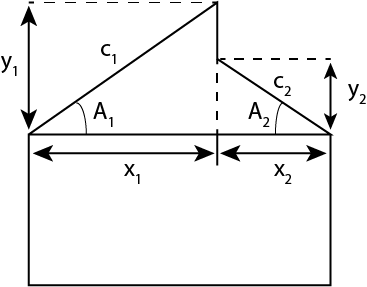
hvor vi kender \(x_1\) og \(x_2\) samt \(y_1\) og \(y_2\) og ud fra dette kan vi beregne vinklerne \(\angle A_1\) og \(\angle A_2\) vha. tangens (se evt. afsnittet om de trigonometriske funktioner). Til sidst vil vi så beregne \(c_1\) og \(c_2\) som er længderne af de nye skrå tagflader.

Den nye totale højde af huset er 7,5 m, mens højden af huset uden tag er 3 m, så vi har at \(y_1 = 7,\!5-3 = 4,\! 5\) m samt at \(y_2 = 5,\!5 - 3 = 2,\! 5\) m. Vi ved også at \(x_1 = 5\) m og derfor må \(x_2 = 8-5 = 3\) m. Vi kan nu beregne vinklerne vha. tangens
$$ 
\begin{align}
A_{1} & = \tan^{-1}\left(\frac{4,\!5}{5}\right) = 42^\circ \ , \\
A_{2} & = \tan^{-1}\left(\frac{2,\!5}{3}\right) = 39,\!81 ^\circ. 
\end{align}
$$

Nu kan vi beregne længden af tagfladerne vha. sinus
$$
\begin{align}
c_{1} & =\frac{4,5}{\sin(42^\circ)}=6,\!7 \ , \\
c_{2} & =\frac{2,5}{\sin(39,\!81^\circ)}=2,\!91.
\end{align}
$$

Den isometriske tegning bliver derved som følgende: