Trekant

Retvinklet trekant

Når vi har med trekanter at gøre, så betegnes arealet ofte med \(T\).

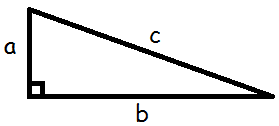
Vi finder arealet af en retvinklet trekant ved at gange de to kateter med hinanden og dividere med to.

$$T=\frac{1}{2}\cdot a\cdot b$$

Læg mærke til, at hvis vi kalder \(b\) for grundlinjen, så er \(a\) højden til \(b\). Derfor kan vi også skrive formlen

$$T=\frac{1}{2}\cdot \mathrm{højde}\cdot \mathrm{grundlinje}$$

$$T=\frac{1}{2}\cdot h\cdot g$$

Lad os prøve at se på, hvorfor formlen ser ud, som den gør.

Hvis vi ”kopierer” vores retvinklede trekant, vender kopien på hovedet og sætter den fast ovenpå den originale, så har vi et rektangel.

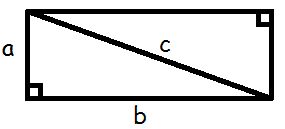
Arealet af to retvinklede trekanter er altså det samme som arealet af et rektangel (længde gange bredde)

$$2T=a\cdot b$$

Vi ganger med en halv på begge sider af lighedstegnet

$$  \frac{1}{\not2}\cdot\not2\cdot T =\frac{1}{2}\cdot a\cdot b$$

$$T =\frac{1}{2}\cdot a\cdot b$$

og så nåede vi frem til formlen.

Vilkårlig trekant

Hvis vi har at gøre med en vilkårlig trekant, så er formlen for arealet faktisk den samme!

$$T=\frac{1}{2}\cdot h\cdot g$$

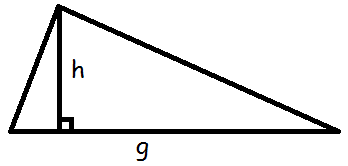
Grunden til at formlen ser sådan ud skyldes, at højden deler trekanten i to retvinklede trekanter.

Vi ved ikke hvor store dele grundlinjen bliver delt i, men hvis vi kalder den lille del for \(x\), så må den store del være resten af grundlinjen (altså grundlinjen foruden \(x\) (\(g-x\))).

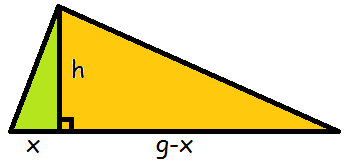
Arealet af trekanten må være arealet af den grønne trekant + arealet af den orange trekant.

Den grønne trekant har kateterne \(x\) og \(h\), derfor bliver arealet

$$T_{\mathrm{grøn}}=\frac{1}{2}\cdot h\cdot x$$

Den orange trekant har kateterne \(h\) og (\(g-x\)), derfor må arealet være

$$T_{\mathrm{orange}}=\frac{1}{2}\cdot h\cdot (g-x)=\frac{1}{2}\cdot h\cdot g-\frac{1}{2}\cdot h\cdot x$$

Når vi lægger dem sammen, får vi arealet af hele trekanten.

$$T=\underbrace{\frac{1}{2}\cdot h\cdot x}_{T_{\mathrm{grøn}}} + \underbrace{\frac{1}{2}\cdot h\cdot g-\frac{1}{2}\cdot h\cdot x}_{T_{\mathrm{orange}}}=\frac{1}{2}\cdot h\cdot g$$

Og sådan er man nået frem til arealformlen.