Reduktion
Ved at bruge de regler, vi har gennemgået i de forrige afsnit, kan man reducere en masse udtryk. Det er derfor en fordel at læse dem igennem først, hvis du har svært ved reduktion.
Et typisk reduktionsstykke kunne være
$$3+(8-2x)-(x+3y)+4y-5$$
Først ophæver vi de to parenteser. Den første er en plusparentes, så der sker ikke noget ved at ophæve den. Den anden er en minusparentes (se evt. afsnit om parenteser), så der skal alle fortegnene skiftes.
$$3\,{\color{Red}{ +(8-2x)}}{\color{Teal}{ -(x+3y)}}+4y-5=3\,{\color{Red}{ +8-2x}}\,{\color{Teal} {-x-3y}}+4y-5$$
Nu sorterer vi leddene, så de rene tal står for sig, leddene med \(x\) står for sig og leddene med \(y\) står for sig. Det må vi gøre, fordi leddenes orden er ligegyldig.
$$3+8-2x-x-3y+4y-5=3+8-5-2x-x-3y+4y$$
Nu skal vi bare lægge de forskellige ting sammen. Det kan være godt at tegne en tallinje, hvor man bevæger sig til venstre ved minus og til højre ved plus.
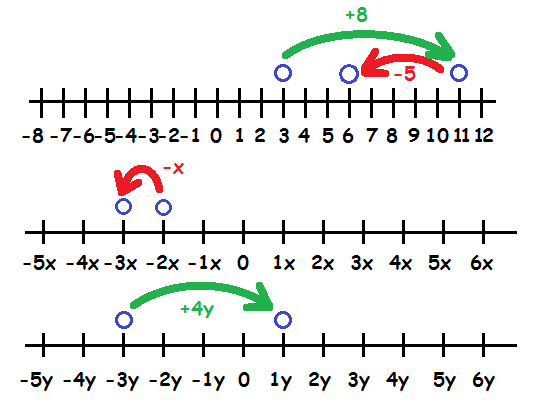
Altså får vi alt i alt
$$3+8-5-2x-x-3y+4y=\underline{\underline{6-3x+y}}$$
Lad os prøve at reducere endnu et stykke
$$a+4(a+2b)-3b(2+a)$$
Vi starter med at gange ind i parenteserne. Vi ganger 4 ind på hvert led i den første parentes
$$a+4(a+2b)-3b(2+a)=a+4a+8b-3b(2+a)$$
Bagefter ganger vi 3\(b\) ind i den anden parentes
$$a+4a+8b-3b(2+a)=a+4a+8b-(6b+3ab)$$
Nu ophæver vi minusparentesen og skifter dermed fortegn på alle led i parentesen.
$$a+4a+8b-(6b+3ab)=a+4a+8b-6b-3ab$$
Nu bytter vi om på leddene, så vi har tallene for sig (der er ingen), leddene med \(a\) for sig, leddene med \(b\) for sig og leddene med \(ab\) for sig.
Leddene står faktisk allerede i denne orden.
Tilbage er der kun at lægge leddene sammen.
$$a+4a+8b-6b-3ab=\underline{\underline{5a+2b-3ab}}$$
Vi slutter afsnittet af med et sidste reduktionsstykke.
$$a(a+3b)-5ab+3(4+a)+4b-5a+2a^2$$
Vi starter med at gange ind i den første parentes. Vi husker, at \(a\cdot a = a^2\).
$${\color{Red} {a(a+3b)}}-5ab+3(4+a)+4b-5a+2a^2$$
bliver til
$${\color{Red} {a^2+3ab}}-5ab+3(4+a)+4b-5a+2a^2.$$
Derpå ganger vi ind i den anden parentes.
$$a^2+3ab-5ab+{\color{Red} {3(4+a)}}+4b-5a+2a^2$$
bliver til
$$a^2+3ab-5ab+{\color{Red} {12+3a}}+4b-5a+2a^2.$$
Nu samler vi de forskellige typer led for sig. Tallene for sig, leddene med \(a\) for sig, leddene med \(b\) for sig, leddene med \(a\) for sig, og leddene med ab for sig.
OBS: Man kan ikke samle leddene med \(a\) og leddene med \(a^2\)! Det ville svare til at lægge cm (der er et længdemål) sammen med cm2 (der er et flademål).
$$12+3a-5a+4b+a^2+2a^2+3ab-5ab$$
Nu lægger vi de enkelte størrelser sammen
$$12+3a-5a+4b+a^2+2a^2+3ab-5ab=\underline{\underline{12-2a+4b+3a^2-2ab}}$$
Igen kan det være en god idé at tegne (eller i hvert fald forestille sig) en tallinje, hvor man bevæger sig til højre eller venstre alt efter, om man lægger til eller trækker fra.
