Omregning: brøk-procent-decimaltal
Fra brøk til procent
Når man skal omregne en brøk til en procentsats, så skal man forlænge eller forkorte brøken således, at der står 100 i nævneren. Dette skyldes, at én procent netop svarer til én hundrededel.
$$\frac{1}{4}=\frac{1\cdot25}{4\cdot25}=\frac{25}{100}=25\%$$
I eksemplet ovenfor har vi forlænget brøken med 25, fordi 4\(\cdot\)25=100.
Det handler altså om at finde ud af, hvilket tal, man skal forlænge med for at få 100 i nævneren.
Hvis man er i tvivl om, hvad man skal forlænge med, så kan man finde det ved at dividere 100 med nævneren. F.eks. er \(\frac{100}{6}=16,666\ldots\)
Derfor er
$$\frac{5}{6}=\frac{5\cdot16{,}66\overline{6}}{6\cdot16,66\overline{6}}=\frac{83{,}33\overline{3}}{100}=83{,}33\overline{3}\%$$
Stregen over tallet betyder, at dette tal gentages uendeligt mange gange.
Fra procent til brøk
Hvis man har fået en procentsats, og man gerne vil skrive den som en brøk, så er det vigtigt at huske, at ”procent” betyder ”hundrededele”. Man kan altså skrive \(x\%\) om til \(\frac{x}{100}\). Herefter gælder det om at finde ud af, om der er nogen tal, der går op i både tæller og nævner. Hvis der er det, kan man forkorte brøken.
$$38\%=\frac{38}{100}=\frac{38:2}{100:2}=\frac{19}{50}$$
I eksemplet ovenfor har vi forkortet med 2, fordi 2 går op i både 38 og 100. Da 19 er et primtal, kan vi ikke forkorte brøken yderligere.
$$64\%=\frac{64}{100}=\frac{64:4}{100:4}=\frac{16}{25}$$
Hvis der er tale om, at procentsatsen er et kommatal, så må man rykke kommaet i både tæller og nævner, før man finder tal, der går op i begge dele.
$$37{,}5\%=\frac{37{,}5}{100}=\frac{375}{1000}$$
Vi ser at 125 går op i både tæller og nævner. Dermed bliver
$$\frac{375}{1000}=\frac{375:125}{1000:125}=\frac{3}{8}$$
37,5% svarer altså til \(\frac{3}{8}\).
Fra brøk til decimaltal
Hvis man har en brøk, man gerne vil omskrive til et decimaltal, så må man dividere brøken ud. Der findes flere metoder til at dividere. Vi gennemgår en her ved hjælp af et eksempel.
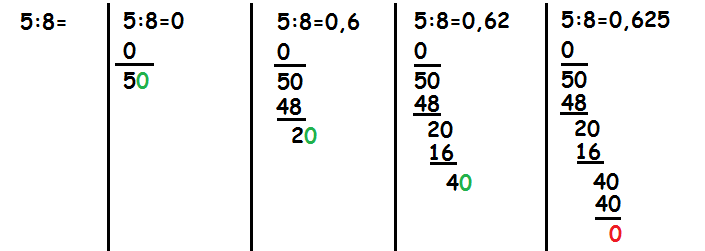
Vil man omskrive \(\frac{5}{8}\) til et decimaltal, så spørger man først hvor mange gange 8 går op i 5. Det er 0 gange. Man skriver dette nul ude til højre. Under femtallet skriver man også 0. Nu trækker man 0 fra 5. Det giver 5. Man hiver et 0 ned (det grønne).
Så spørger man, hvor mange gange 8 går op i 50. Det er 6 gange. Man skriver 6-tallet ude til højre, og man skriver resultatet af 6\(\cdot\)8 under 50. Ved at trække 48 fra 50 får vi 2. Vi trækker endnu et nul ned.
Så spørger vi, hvor mange gange 8 går op i 20. Det er 2 gange. Vi skriver 2-tallet ude til højre of resultatet af 8\(\cdot\)2 under 20. Vi trækker 16 fra 20 og får 4. Vi trækker et nul ned.
Til sidst spørger vi, hvor mange gange 8 går op i 40. Det er 5 gange. Vi skriver 5 ude til højre, og skriver 5\(\cdot\)8 under 40. Nu står der 40-40, og det giver 0. Når der står 0 forneden er vi færdige.
\(\frac{5}{8}\) svarer altså til 0,625.
Fra decimaltal til brøk
Hvis man vil omskrive et decimaltal til en brøk, så er der to tilfælde, man kan se på. Det første tilfælde hvor der er endeligt mange cifre (f.eks. 0,125 eller 4,3), og det andet tilfælde, hvor der er et tal, der går igen og igen uendeligt mange gange (f.eks. 0,3333333333\(\ldots\)).
I det første tilfælde omskriver man decimaltallet ved i tælleren at skrive tallet, hvor man blot har fjernet kommaet. I nævneren skriver man et 1-tal efterfulgt af så mange 0’er som der er pladser efter kommaet. Herefter kan man forkorte brøken.
$$0{,}125=\frac{125}{1000}=\frac{125:125}{1000:125}=\frac{1}{8}$$
I eksemplet ovenfor skrev vi 1000 i nævneren, fordi der er 3 cifre efter kommaet i 0,125.
Hvis man er i det andet tilfælde, hvor der er et tal, der gentages uendeligt mange gange, så skal man forlænge med 9, 99, 999,… alt efter hvor mange cifre, der er i det tal, der gentages i det uendelige. Tælleren bliver så de cifre, der gentages, mens nævneren bliver det, man har forlænget med.
Eksempelvis bliver
$$0{,}44444\overline{4}=\frac{0{,}44444\overline{4}\cdot9}{9}=\frac{4}{9}$$
$$0{,}43274327\overline{4327}=\frac{0{,}43274327\overline{4327}\cdot9999}{9999}=\frac{4327}{9999}$$
Her bruger vi, at
$$0{,}3333\overline{3}\cdot9=3$$
$$0{,}8888\overline{8}\cdot9=8$$
$$0{,}171717\overline{17}\cdot99=17$$
$$0{,}123123123\overline{123}\cdot999=123$$
Fra procent til decimaltal
Hvis man vil omskrive en procentsats til et decimaltal, skal man huske, at ”procent” betyder ”hundrededele”. At finde en hundrededel svarer til at dividere med 100, og det svarer igen til at rykke kommaet to pladser til venstre.
$$98\%=0{,}98$$
$$120\%=1{,}20$$
$$34{,}87\%=0{,}3487$$
Fra decimaltal til procent
Her gør man det omvendte af ovenfor. Man rykker kommaet to pladser til højre
$$0{,}17=17\%$$
$$1{,}456=145{,}6\%$$
$$0{,}1112=11{,}12\%$$
Videolektion
