Blandede tal

Det sker, at tælleren er større end nævneren i en brøk. I så fald kan man omskrive brøken til et blandet tal. Dvs. et tal, der både indeholder heltal og brøker.

F.eks er

$$\frac{4}{3}=1\tfrac{1}{3}.$$

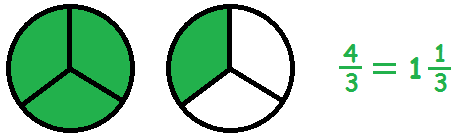
Man finder det hele tal ved at se, hvor mange gange nævneren går op i tælleren.

Den rest, der er tilbage, bliver stående i tælleren.

Bemærk, at der IKKE er et skjult gangetegn mellem det hele tal og brøken i et blandet tal. Der er snarere et skjult plustegn.

Lad os for eksempel omskrive \(\frac{13}{4}\) til et blandet tal.

Først skal vi finde ud af, hvor mange gange 4 går op i 13. 4 går op i 13 3 gange (4\(\cdot\)3=12) og der er en rest på 1. Dermed er

$$\frac{13}{4}=3\tfrac{1}{4}.$$

Fra blandet tal til brøk

Hvis man vil omskrive et blandet tal til en brøk, så kan man ”forlænge” det hele tal med nævneren. Dvs. man laver en ny brøk, hvor man skriver nævneren fra den gamle brøk i nævneren og det hele tal ganget med den gamle nævner i tælleren. Derefter lægger man den nye brøk sammen med den gamle.

Eksempler:

$$7\tfrac{2}{3}=\frac{7\cdot3}{3}+\frac{2}{3}=\frac{21}{3}+\frac{2}{3}=\underline{\underline{\frac{23}{3}}}$$

$$2\tfrac{7}{8}=\frac{2\cdot8}{8}+\frac{7}{8}=\frac{16}{8}+\frac{7}{8}=\underline{\underline{\frac{23}{8}}}$$