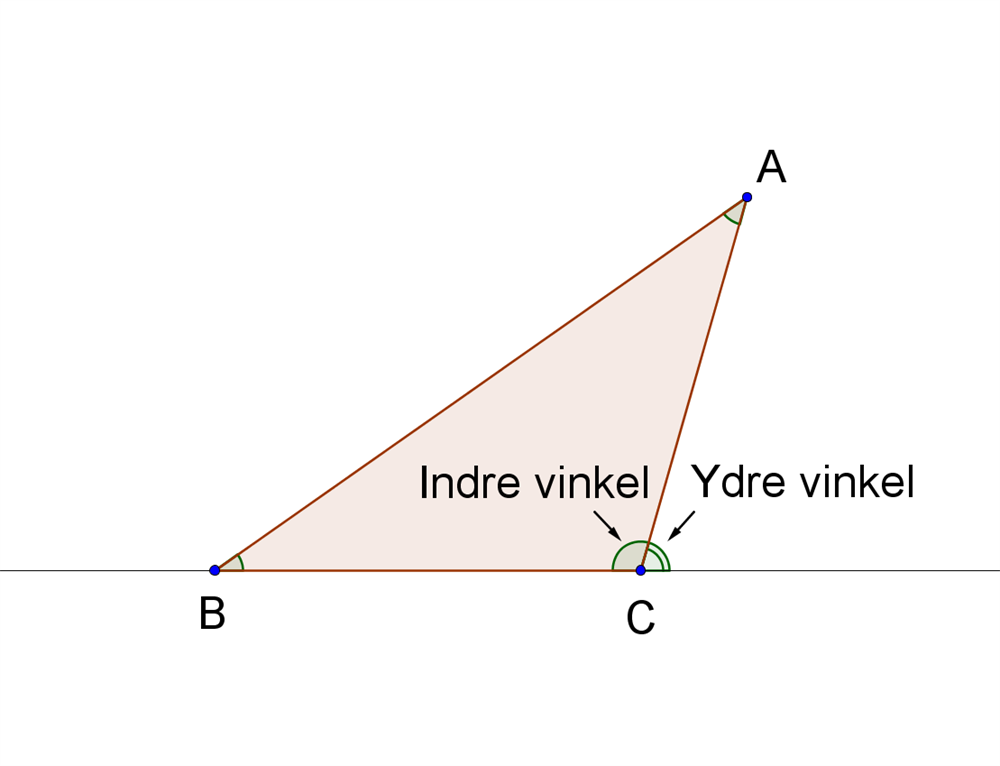
Vilkårlig trekant

Vilkårlige trekanter er alle polygoner, der har tre sider og en vinkelsum på 180 grader. En vilkårlig trekant er derfor en hvilken som helst trekant, du kan forestille dig på en flad overflade. Retvinklede trekanter er derfor et specialtilfælde af vilkårlige trekanter. 

For de vilkårlige trekanter, der ikke indeholder rette vinkler, er man nødt til at bruge enten sinusrelationen eller cosinusrelationen for at beregne sider og vinkler. Hvilket udtryk man bruger afhænger af de givne oplysninger. Sinusrelationen er defineret nedenunder.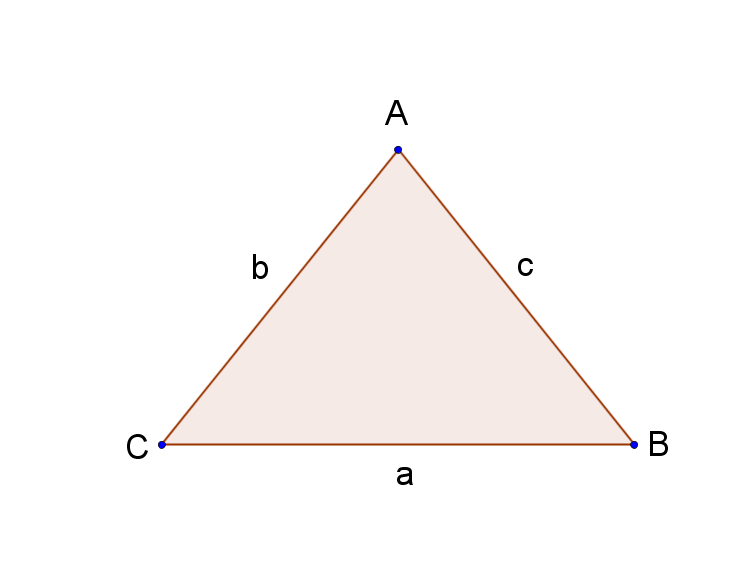

$$\begin{equation}
\frac{a}{\sin(A)} = \frac{b}{\sin(B)} = \frac{c}{\sin(C)}
\end{equation}$$
For at anvende sinusrelationen udvælger man 2 ud af de 3 brøker i relationen.

Anvendelsesområder

• Man kender 2 vinkler og en side
• Man kender 2 sider og en vinkel, hvor siderne ikke danner den kendte vinkel

Cosinusrelationen er defineret som
$$\begin{align}
a^2 & =b^2 + c^2 - 2bc \cdot \cos(A)\\
b^2 & =a^2 + c^2 - 2ac \cdot \cos(B)\\
c^2 & =a^2 + b^2 - 2ab \cdot \cos(C)
\end{align}$$

Anvendelsesområder

• Man kender 3 sider
• Man kender 1 vinkel og de 2 sider der danner vinklen

Eksempel 1 - beregn vinkel

\(a=5, \angle{A} = 30^{\circ}, c = 4\), beregn \(\angle{C}\). Her kender vi 2 sider og en vinkel. Hvis vi benytter ovenstående tegning, fremgår det at de to sider ikke danner vinklen og vi kan derfor benytte sinusrelationen.

$$\begin{eqnarray*}
\frac{a}{\sin(A)} = \frac{c}{\sin(C)} &\, \Leftrightarrow \, & \frac{a}{\sin(A)} \cdot \sin(C) = c \, \Leftrightarrow \, \\ \sin(C) = \frac{c \cdot \sin(A)}{a} &\, \Leftrightarrow \, & \sin^{-1}(\sin(C)) = \sin^{-1}\left(\frac{c \cdot \sin(A)}{a})\right) \\ C = \sin^{-1}\left(\frac{4 \sin(30)}{5}\right) &=& \sin^{-1}(0.4)=23.6^{\circ}
\end{eqnarray*}$$

Eksempel 2 - beregn vinkel

\(b=1.2, \angle{A} = 60^{\circ}, c\) = 4.5, beregn \(\angle{C}\). Igen kender vi 2 sider og en vinkel, men her danner de 2 sider vinklen og vi kan derfor ikke benytte sinusrelationen, men cosinusrelationen. Med de givne oplysninger kan vi ikke finde \(\angle{C}\) direkte, men vi må bruge 2 trin. Trin 1 er at bestemme \(a\). Trin 2 er ved hjælp af \(a\) at bestemme\(\angle{C}\).

$$\begin{eqnarray*}
a^2=b^2 + c^2 - 2bc \cdot \cos(A) & = & 1.2^2 + 4.5^2 - 2 \cdot 1.2 \cdot 4.5 \cdot \cos(60) \\
&=& 16.3 \ \Leftrightarrow \ \\ a&=&4.04
\end{eqnarray*}$$

Trin 2 er at bestemme \(\angle{C}\), som dog kræver at vi omskriver cosinusrelationen lidt.

$$\begin{eqnarray*}
c^2 & = & a^2 + b^2 - 2ab \cdot \cos(C)  \Leftrightarrow \\
c^2 - a^2 - b^2 & = & - 2ab \cdot \cos(C) \Leftrightarrow \\
\frac{c^2 - a^2 - b^2}{-2ab} & = & \cos(C) \Leftrightarrow \\
\frac{a^2 + b^2 - c^2}{2ab} & = & \cos(C) \Leftrightarrow \\
C & = & \cos^{-1}\left(\frac{a^2 + b^2 - c^2}{2ab}\right) = \cos^{-1}\left(\frac{4.04^2 + 1.2^2 - 4.5^2}{2 \cdot 4.04 \cdot 1.2}\right) \\
& = & 105^{\circ}
\end{eqnarray*}$$

Bemærk: Efter at have bestemt \(a\), kunne vi have valgt at bruge sinusrelationen i trin 2. Hvis vi havde gjort dette havde vi fået

$$\begin{eqnarray*}
\frac{a}{\sin(A)} = \frac{c}{\sin(C)} \, \Leftrightarrow \, C = \sin^{-1}\left(\frac{c\sin(A)}{a}\right) = \sin^{-1}\left(\frac{4.5 \cdot \sin(60)}{4.04}\right) = 75^{\circ}
\end{eqnarray*}$$

I trekanter med en stump vinkel skal man være forsigtig med at bruge sinusrelationen, da \(\sin(180-v)=\sin(v)\) og der dermed kan være to løsninger på problemet. Hvis man bruger lommeregneren får man den spidse vinkel, som i figuren er vinklen på ydersiden af trekanten. Den stumpe vinkel fås ved \(180^{\circ}-v\). hvilket i eksemplet ovenfor ville have givet \(180^{\circ}-75^{\circ}=105^{\circ}\) og dermed den indre stumpe vinkel.