Firkanter

Begrebet firkant dækker alle de geometriske figurer der har a) fire sider og b) fire vinkler. Yderligere gælder der at

1. Summen af vinkler i en firkant altid er \(360^{\circ}\).
2. Hver firkant har to diagonaler.

Diagonaler var ikke noget vi så til i kapitlerne om trekanter (og ikke vil i kapitlerne i cirkler) da man har brug for mindst fire hjørner for at kunne definere en diagonal. Dette skyldes at diagonalen forbinder to hjørner som ikke er nabohjørner (se billedet nedenunder).

Forskellige slags firkanter

At skelne de mange firkantede konstruktioner kan virke uoverskueligt, men alt vi behøver er at kigge på deres sider, vinkler og diagonaler.

Rektangel

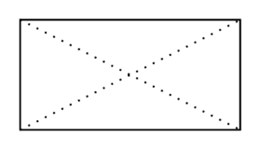
I et rektangel gælder der at

1. De fire vinkler er rette.
2. Siderne er parvis parallelle.
3. Diagonalerne krydser i dens midtpunkt.

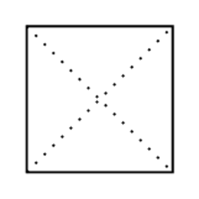
Kvadrat

I et kvadrat gælder der at

1. De fire vinkler er rette.
2. Alle sider er lige lange.
3. Siderne er parvis parallelle.
4. Diagonalerne krydser i dens midtpunkt.
5. Diagonalerne er vinkelrette på hinanden.

Det er værd at bemærke at et kvadrat faktisk er et specialtilfælde af rektanglet. 

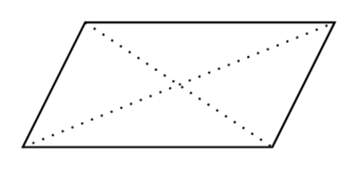
Parallelogram

I et parallelogram gælder der at

1. Summen af to nabovinkler er \(180^{\circ}\).
2. Siderne er parvis parallelle.
3. Diagonalerne krydser i dens midtpunkt.

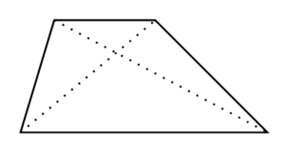
Trapez

I en trapez gælder det, at

1. Kun ét par af siderne er parallelle

Der findes også ligebenede trapezer hvor de to ikke-parallelle sider er lige lange. Hvis det var de to parallelle sider, der var lige lange, så vil de to andre sider også blive parallelle og vi ville ende med et rektangel eller et parallellogram.