Kasse

En kasse, der er sammensat af rektangler (dvs. alle vinkler er 90 grader) er let at beregne rumfanget af. Man ganger simpelthen bare længde, bredde og højde med hinanden.

$$V_{\mathrm{kasse}}=l\cdot b\cdot h$$

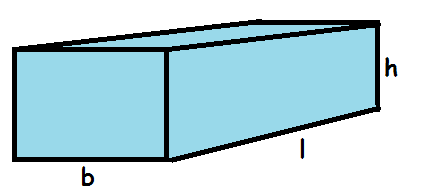
Kassens overflade består af 6 sider, der er parvist lige store. Overfladearealet, \(A\), er derfor

$$A_{\mathrm{kasse}}=2\cdot b\cdot h+2\cdot l\cdot b+2\cdot l\cdot h = 2(bh+lb+lh)$$

Parallelogram endestykker

Man kunne også forestille sig en kasse, hvor endestykkerne er parallelogrammer.

I så fald skal man finde arealet af grundfladen og gange med figurens højde.

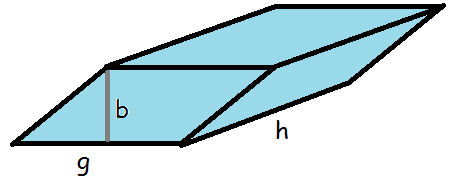
Her skal man holde tungen lige i munden.

Der er nemlig dels kassens højde (markeret med \(h\)) og så er der højden i parallelogrammet, der markeres med \(b\) for at kende forskel. Parallelogrammets areal er højde gange grundlinje.

Vi udregner altså rumfang således:

$$V_{\mathrm{parallelogram}}=\mathrm{grundflade}\cdot \mathrm{højde}$$

$$V_{\mathrm{parallelogram}}= b\cdot g\cdot h$$

Trapez endestykker

Hvis vi havde at gøre med en kasse, hvis grundflade var et trapez, ville vi også skulle gange kassens højde med grundfladens areal for at få rumfanget.

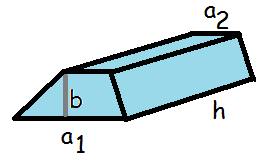
Her er arealet af grundfladen (se evt. afsnittet om trapez)

$$A_{\mathrm{grundflade}}=\frac{1}{2}\cdot b\cdot(a_1+a_2)$$

Så rumfanget bliver

$$V_{\mathrm{trapez}}=\mathrm{højde}\cdot \mathrm{grundflade}$$

$$V_{\mathrm{trapez}}=\frac{1}{2}\cdot b\cdot h\cdot(a_1+a_2)$$