Lineær funktion

Mange af de sammenhænge, man støder på, er lineære. Det betyder, at deres graf er en ret linje.

De lineære funktioner ser ud på en bestemt måde. Sammenhængen mellem \(x\) og \(y\) er

$$y=a\cdot x+b$$

\(a\) og \(b\) er to konstanter.

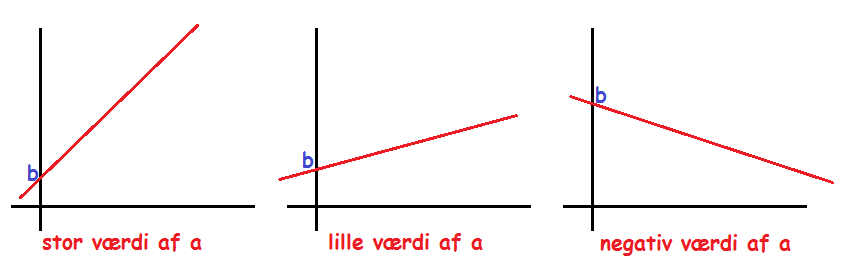
\(a\) bestemmer noget om hældningen på funktionens graf (hvor stejlt den vokser/aftager)

\(b\) bestemmer noget om, hvor på \(y\)-aksen grafen starter.

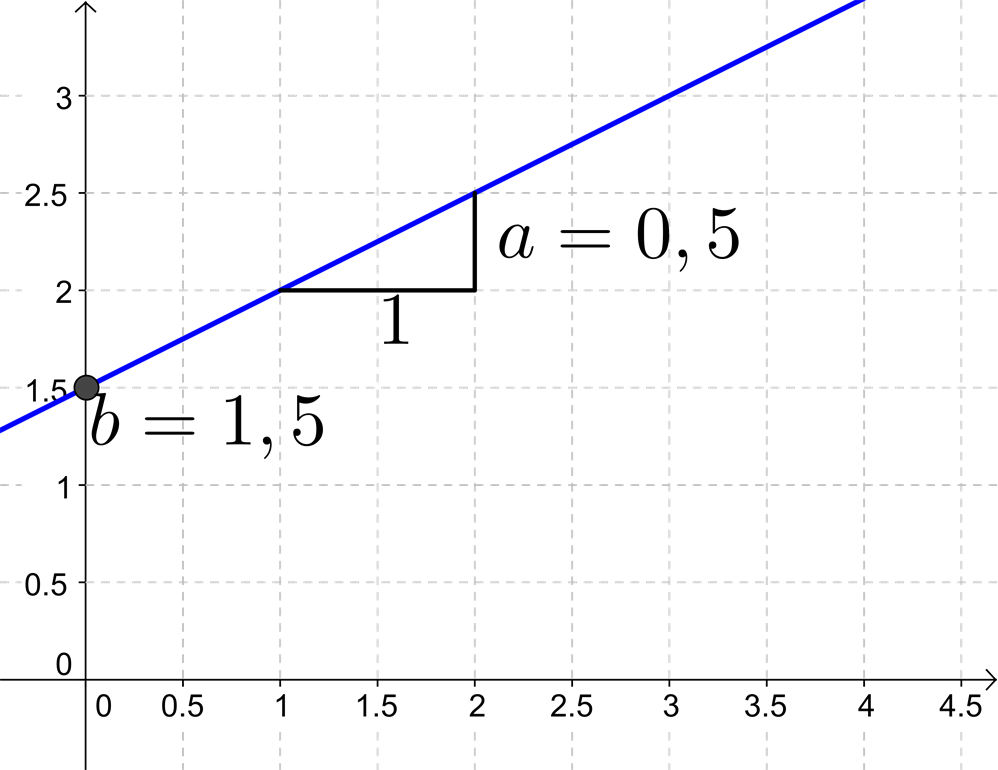
Hvis man har grafen for en lineær funktion, så kan man aflæse værdierne af \(a\) og \(b\).

Man aflæser \(a\) ved at starte et tilfældigt sted på grafen. Så går man 1 hen ad \(x\)-aksen. Den ændring, der er på \(y\)-aksen er lig med \(a\).

\(b\) aflæser man der hvor grafen skærer \(y\)-aksen.

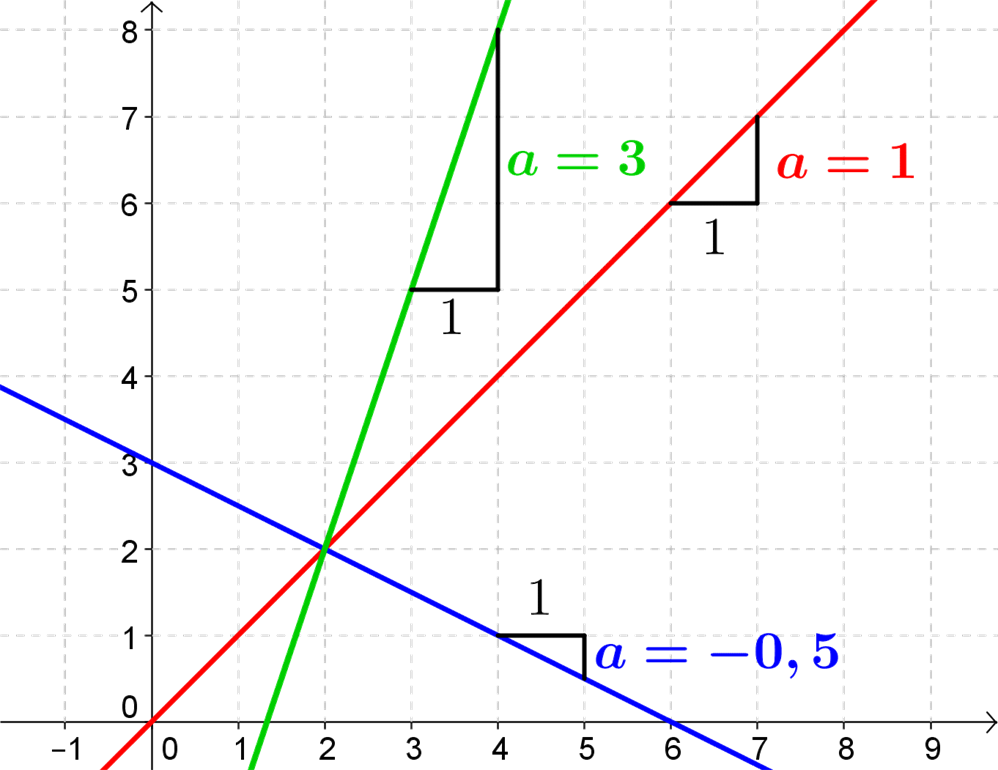
Her kan du se nogle grafer for lineære funktioner med forskellige \(a\)-værdier