Hvad er en funktion?
En funktion beskriver sammenhængen mellem to ting (to størrelser). Ofte er det nemlig sådan, at når én størrelse ændres, så ændres en anden også.
Et eksempel kunne være en varm kop te. Når tiden går, bliver teen koldere. Der er altså her tale om en sammenhæng mellem tid og temperatur. Matematisk siger man, at ”teens temperatur er en funktion af tiden”.
Man kunne også have set på mængden af bobler i en sodavand som funktion af tiden, eller på folks skostørrelse som funktion af deres højde, eller på en bils bremselængde som funktion af dens hastighed.
Funktioner er et værktøj til at hitte styr på den slags sammenhænge.
Variable
De størrelser, der er en sammenhæng mellem, og som man vil lave en funktion om, kaldes variable. Det gør de, fordi de kan variere (ændre sig).
De to variable, der indgår i en variabelsammenhæng kaldes henholdsvis uafhængig og afhængig.
Den uafhængige variable har vi lov at bestemme over. Den afhængige variable bliver bestemt af funktionen, når vi har valgt den uafhængige.
Funktionsudtryk
Man kalder tit den uafhængige variable for \(x\), og den afhængige variable for \(y\).
En sammenhæng mellem de to variable kunne f.eks. være
$$y=6\cdot x$$
Vi bestemmer selv, hvilke værdier, vi kommer ind på \(x\)’s plads, og så kan vi udregne, hvad \(y\) bliver.
Hvis vi sætter \(x=1\), så bliver \(y=6\). Hvis vi sætter \(x=3\), så bliver \(y=6\cdot3=18\).
Funktionen ovenfor kunne være en model over køb af kartofler til 6 kr./kg., hvor \(x\) er antal kilogram og \(y\) er prisen.
Man kan sætte værdierne op i et skema, et såkaldt sildeben.
| x (kg. kartolfer) | y (pris i kr.) |
| 1 | 6 |
| 2 | 12 |
| 3 | 18 |
| 4 | 24 |
| 7 | 42 |
| 10 | 60 |
Graf
Man kan også indtegne punkterne i et koordinatsystem.
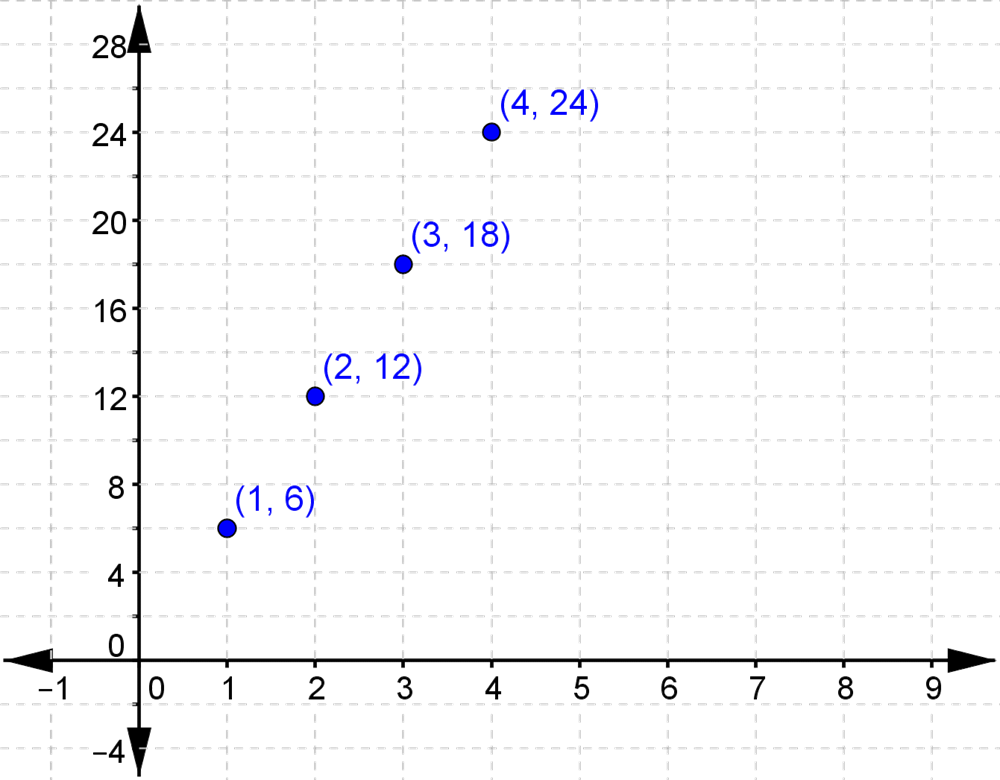
Hvis man prøvede at indsætte en masse forskellige \(x\)-værdier (også decimaltal), ville vi til sidst få en kurve frem. Det er den, der kaldes funktionens graf.
Ud fra en bestemt x-værdi kan man gå lodret op til grafen og så gå vandret hen til \(y\)-aksen for at aflæse den tilhørende \(y\)-værdi.
Hvis man nu vil købe 3 kg kartofler, så går man lodret op fra 3 på \(x\)-aksen. Når man rammer grafen er man nået 18 op. Prisen for 3 kg kartofler er altså 18 kr.
