Pyramide

En pyramide er en figur, der har en grundflade, hvor hvert af grundfladens hjørner er forbundet til et punkt, der ligger over grundfladen.

Grundfladen kan eksempelvis være trekantet eller firkantet, som det ses på tegningerne, men kan også have flere kanter (den skal altså være en polygon. Polygon er det græske ord for mangekant).

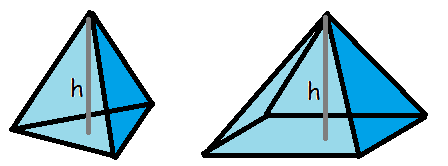
Det forholder sig ligesom med keglen, at rumfanget af en pyramide er en tredjedel af den tilsvarende kasse/prisme. Altså højden gange grundfladens areal divideret med 3.

$$V_{\mathrm{pyramide}}=\frac{\mathrm{A_{\mathrm{grundflade}}}\cdot \mathrm{højde}}{3}$$

Overfladearealet af en pyramide findes ved at lægge grundfladearealet sammen med de trekantede sidefladers samlede areal. Du kan finde arealet af en trekant med $$A_{\mathrm{trekant}}=\frac{1}{2}\cdot h_{\mathrm{trekant}}\cdot g$$Vær opmærksom på de to forskellige højder: Pyramidens højde og trekantens højde. 

En regulær polygon er en polygon, hvor alle sider er lige lange.

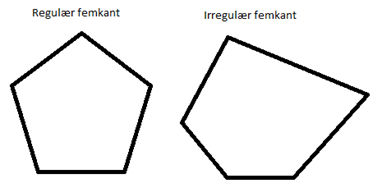
Hvis en pyramide har en regulær polygon som grundflade, og polygonen har n sider (der alle har længden g), kan overfladearealet A for pyramiden findes ved

$$A_{\mathrm{pyramide}}= A_{\mathrm{grundflade}} + n \cdot \frac{1}{2}\cdot h_{\mathrm{trekant}}\cdot g$$ 

Hvis pyramiden har en irregulær polygon som grundflade, er man nødt til at udregne arealet af hver trekant for sig og lægge alle disse arealer sammen med arealet af grundfladen.