Retvinklet trekant

Vi skal starte med den retvinklede trekant, dvs. en trekant hvor en af vinklerne er \(90^{\circ}\). I trekanten \(ABC\) er vinklen \(\angle{C} = 90^{\circ}\).

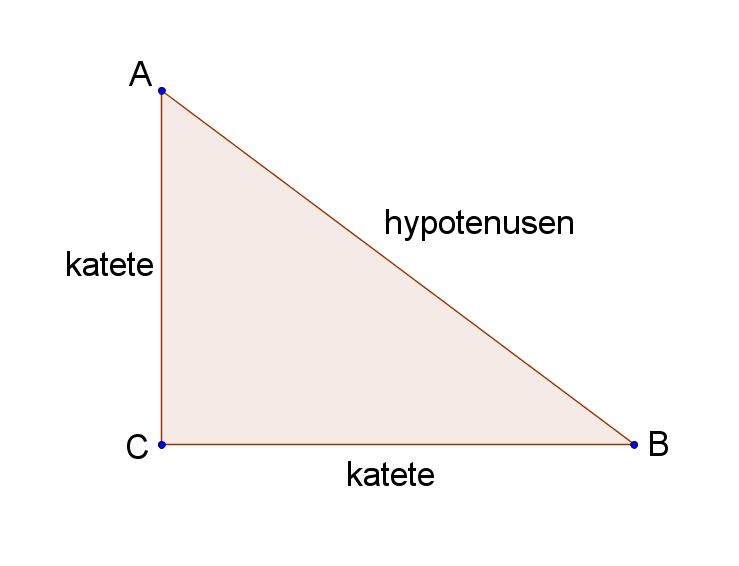
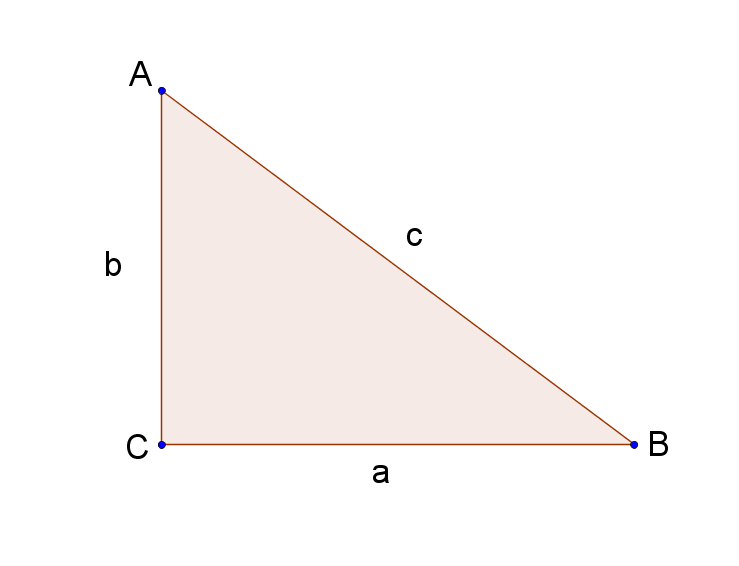
Her kan funktionerne cosinus, sinus og tangens defineres som

$$\begin{align}
\cos(v) & = \frac{\mathrm{hosliggende} \ \mathrm{katete}}{\mathrm{hypotenusen}} \\
\sin(v) & = \frac{\mathrm{modstående} \ \mathrm{katete}}{\mathrm{hypotenusen}} \\
\tan(v) & = \frac{\mathrm{modstående} \ \mathrm{katete}}{\mathrm{hosliggende} \ \mathrm{katete}}
\end{align}$$

for en arbitrær vinkel \(\angle{v}\). Erstatter vi \(\angle{v}\) med \(\angle{A}\) i trekanten \(ABC\), kan ovenstående definitioner omskrives til

$$\begin{equation}
\cos(A) = \frac{b}{c} \qquad
\sin(A) = \frac{a}{c} \qquad
\tan(A) = \frac{a}{b}
\end{equation}$$

Dvs. den overfor liggende side til \(\angle{A}\) betegnes \(a\) og så fremdeles. For nogen vil det være nemmere at beskrive sidelængderne ved hjælp af punkterne \(A\), \(B\) og \(C\). Sidelængden \(a\) er længden fra punkt \(B\) til \(C\), som kort kan skrives sidelængden \(|BC|\).

Bruger vi istedet \(\angle{B}\) som udgangspunkt fås

$$\begin{align}
\cos(B) & = \frac{a}{c} = \frac{|BC|}{|AB|}\\
\sin(B) & = \frac{b}{c} = \frac{|AC|}{|AB|}\\
\tan(B) & = \frac{b}{a} = \frac{|AC|}{|BC|}
\end{align}$$
Dvs. man skal bruge to kendte størrelser for at beregne den tredje.

Eksempel 1 - Beregn sidelængde

Vi ved at \(a=5, \angle{A} = 30^{\circ}\) og ønsker at beregne \(c\).

Vi skal finde et udtryk som indeholder alle 3 størrelser. Dette gør udtrykkket \(\sin(A)\), hvori vi kan isolere \(c\), indsætte de oplyste værdier og udregne det med lommeregner/CAS.

$$\begin{eqnarray}
\sin(A) & = & \frac{a}{c} \Leftrightarrow\\
c \cdot \sin(A) & = & a \Leftrightarrow \\
c & = & \frac{a}{\sin(A)} = \frac{5}{\sin(30)} = 10
\end{eqnarray}$$

Eksempel 2 - beregn vinkel

Vi ved at \(b=2, c=4\) og ønsker at beregne \(\angle{A}\).

Udtrykket \(\cos(A)\) indeholder alle 3 størrelser.

$$\begin{eqnarray}
\cos(A) & = & \frac{b}{c} \Leftrightarrow\\
\cos^{-1}(\cos(A)) & = & \cos^{-1}\left( \frac{b}{c}\right) \Leftrightarrow\\
A & = & \cos^{-1}\left(\frac{b}{c}\right) = \cos^{-1}\left(\frac{2}{4}\right)= 60^{\circ}
\end{eqnarray}$$

Bemærk: I udregningen benytter vi \(\cos^{-1}\) som er invers cosinus, som findes på de fleste lommeregnere. Når man anvender en invers funktion på funktionen selv får man 1 dvs. \(\cos^{-1}(\cos(A))=A\). Dette var for funktioner, men noget lignende gør sig gældende for tal, hvor eksempelvis $$2^{-1} \cdot 2=\frac{1}{2} \cdot 2 = \frac{2}{2} = 1 \ .$$