Ohms lov - Elektriker

En vigtig og meget anvendelig ligning til udregning af forhold i elektriske kredsløb er eksempelvis ohms lov. 

$$ U =R \cdot I $$

hvor U er spændingen, R er modstanden og I er strømstyrken. 

Ud fra denne lov kan vi altså eksempelvis bestemme spændingsforksellen over en kredsløbskomponent, så længe vi kender modstanden i komponenten samt strømmen igennem den. 

Eksempelvis:

 

 

 

 

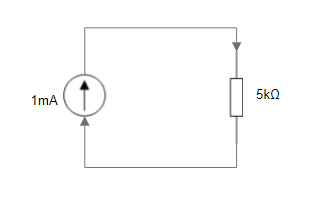
I det tegnede kredsløb er strømmen \( 1mA \) og modstanden i resistoren er \( 5k\Omega \). Så kan vi nemt benytte Ohms lov til at bestemme spændingen over resistoren.

$$ 5k\Omega \cdot 1mA = 5V $$

Da Ohms lov er en ligning, så må vi gerne bytte om på enhederne, bare vi sørger for, at gøre det på begge sider af lighedstegnet. Den kan f.eks. skrives som

$$ R = \frac{U}{I} $$

Her er det f.eks. muligt at bestemme en modstand, hvis man kun kender strømstyrken og spændingen. 

 

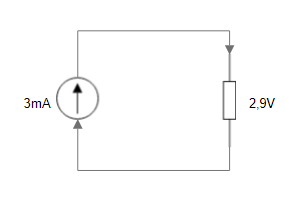
Her kan vi, ved hjælp af Ohms lov, finde hvor stor resistoren er i kredsløbet.

$$ \frac{2.9V}{3mA} = 0.96k\Omega $$

Vi kan altså bruge Ohms lov til at bestemme spænding, modstand og strømstyrke, så længe mindst to af dem er kendt. 

Ohms lov viser også, at spænding, strømstyrke og modstand er tæt relateret til effekt. Dette kan udtrykket ved 

$$ P = U \cdot I $$

Hvor P er effekten. Effekt har enheden watt(W), hvilket er joules pr. sekund. Det er altså de energi der bliver leveret i et kredsløb hvert sekund. Kender man to af de fire variable, så kan man finde de to ukendte. 

Et eksempel: 
Vi kender modstanden og strømmen i et kredsløb, men ønsker at bestemme spænding og effekt. Vi benytter to udtryk,

$$ U = R \cdot I \, \text{og} \, P = U \cdot I $$

Hvis vi indsætter udtrykket for \( U \) i udtrykket \( P = U \cdot I \), så får vi følgende

$$ P = R \cdot I \cdot I = R \cdot I^2 $$

Nu har vi altså fundet en nem måde, at bestemme effekten, bare ved at kende modstand og strømstyrke.

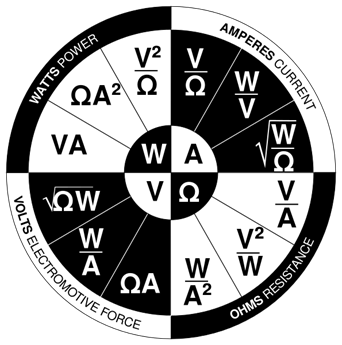I figuren vises alle de forskellige sammenhæng mellem strøm, spænding, modstand og effekt. Husk at de fire størrelser har enhederne \( V = [\mathrm{U}] \), \( A = [\mathrm{I}] \), \( \Omega = [\mathrm{R}] \) og \( W = [\mathrm{P}] \).

Prøv selv at udlede nogle af udtrykkene, og se hvordan de fire variable hænger sammen.

 

 

Kilde: Per Mejdal Rasmussen.