Målestoksforhold - Tømrer

Når der arbejdes på store byggepladser, er det praktisk at have en teknisk tegning af det, der skal bygges. En teknisk tegning kan se ud, som vist på billedet nedenfor.

Forestil dig for eksempel dit hus eller rådhuset i din by. Det ville være ret upraktisk, hvis tegningerne af disse bygningner skulle være lige så store som selve bygningerne. Derfor anvender man målestoksforhold. På den måde kan man tegne store bygninger på små papirer.

Nedenfor gennemgår vi, hvordan målestoksforhold anvendes i forbindelse med tekniske tegninger. Skulle du blive i tvivl undervejs om, hvad målestoksforhold betyder, eller hvor formlerne kommer fra, kan du læse vores side om målestoksforhold. 
Inden vi går i gang med eksemplerne gennemgår vi dog nogle huskeregler om målestoksforhold. 

Hvis vi har fået en tegning angivet i målestoksforholdet \(1:100 \) betyder dette at "1 enhed på tegningen svarer til 100 enheder i virkeligheden". Hvis tegnigen f.eks. er angivet i cm betyder det altså at "1 cm på tegningen svarer til 100 cm i virkeligheden". 

Hvis vi skal finde længden af en væg i virkeligheden, når vi kun har tegningen, kan vi også anvende målestoksforholdet. Hvis målestoksforholdet er \(1:100 \) og en væg på tegningen er \(4 cm\), ganger vi med den del der svarer til "100 enheder i virkeligheden". Altså:
$$4 \mathrm{cm} \cdot100 = 400 \mathrm{cm} = 4 \mathrm{m}$$

Her har vi brugt at 1 m svarer til 100 cm. Hvis vi omvendt gerne vil vide hvor meget længden af væggen svarer til på tegningen, skal vi dividere med den del der svarer til "100 enheder i virkeligheden". Altså:
$$\frac{4\mathrm{m}}{100}  = 0,04 \mathrm{m} = 4 \mathrm{cm}$$

Nu er vi klar til eksemplerne

Eksempler

1: Fra virkelighed til tegning

Vi har fået givet følgende skitsetegning af en bygning, der skal opføres: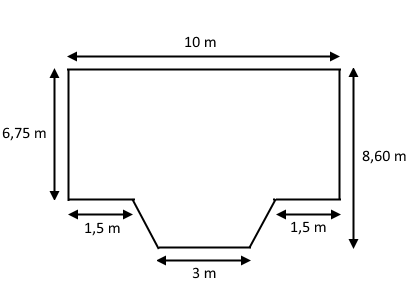

Opgaven lyder på at konstruere en tegning af bygningen i målestoksforholdet \(1:100 \). 

For at gøre det mere overskueligt farvelægger vi væggene i forskellige farver: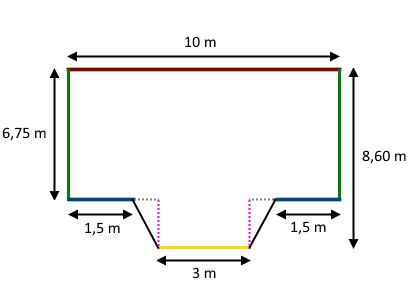

Den grå og pink linje vender vi tilbage til. Da vi skal finde ud af hvor meget væggene svarer til på tegningen, skal vi dividere med 100. Vi får:
Rød væg: \( \frac{10\mathrm{m}}{100} = 0,1 \mathrm{m} = 10 \mathrm{cm} \)
Gul væg: \( \frac{3\mathrm{m}}{100} = 0,3 \mathrm{m} = 3 \mathrm{cm} \)
Hver grøn væg: \( \frac{6,75\mathrm{m}}{100} = 0,0675 \mathrm{m} = 6,75 \mathrm{cm} \) 
Hver blå væg: \( \frac{1,5\mathrm{m}}{100} = 0,015 \mathrm{m} = 1,5 \mathrm{cm} \)
Det eneste, vi nu mangler, er at finde ud af, hvordan den gule væg skal tegnes i forhold til de blå vægge. Dette bestemmer den pink og grå linje. Den gule væg skal placeres med en afstand svarende til den grå linje væk fra de blå vægge, og med en afstand svarende til den pink linje under de blå vægge. 

Hvis vi ser på tegningen, kan vi se, at hvis vi lægger længderne af de blå vægge, længderne af de to grå linjer samt længden af den gule væg sammen, får vi hvad der svarer til længden af den røde væg. Altså:
$$(2\cdot1,5\mathrm{m}) + (2\cdot \mathrm{grå} \ \mathrm{linje}) + 3 \mathrm{m} = 10 \mathrm{m} \\
2\cdot \mathrm{grå} \ \mathrm{linje} = 10 \mathrm{m}  - (2\cdot1,5\mathrm{m}) - 3\mathrm{m} \\
\mathrm{grå} \ \mathrm{linje} = \frac{10 m  - (2\cdot1,5\mathrm{m}) - 3\mathrm{m}}{2} \\
\mathrm{grå} \ \mathrm{linje} = \frac{4 \mathrm{m}}{2} = 2 \mathrm{m} $$
Altså svarer en grå linje til 2 m i virkeligheden.  På tegningen bliver det:
$$ \frac{2\mathrm{m}}{100} = 0,02 \mathrm{m} = 2 \mathrm{cm} $$

For den pink linje kan vi se at, hvis vi lægger længden af en grøn væg til længden af en pink linje får vi 8,6 m. Dvs:
$$ 6,75 \mathrm{m} + \mathrm{pink} \ \mathrm{linje} = 8,6 \mathrm{m}  \\
\mathrm{pink} \ \mathrm{linje} = 8,6 \mathrm{m} - 6,75 \mathrm{m} \\
\mathrm{pink} \ \mathrm{linje} = 1,85 \mathrm{m} $$
Altså svarer en pink linje til 1,85 m i virkeligheden. På tegningen bliver det:
$$ \frac{1,85\mathrm{m}}{100} = 0,0185 \mathrm{m} = 1,85 \mathrm{cm} $$

Altså skal den gule væg på tegningen placeres 2 cm til højre og venstre for de blå vægge og 1,85 cm under de blå vægge. Alle mål fra skitsetegningen er nu omsat i målestoksforholdet \(1:100\) og det er nu muligt at konstruere tegningen som ser ud som vist nedenfor.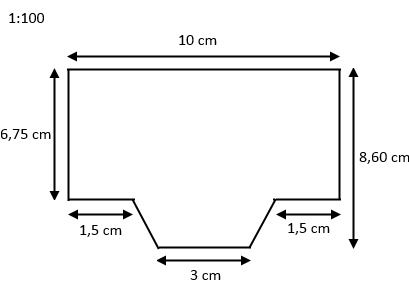

2: Fra tegning til virkelighed

 En bygning har følgende tekniske tegninger med målestoksforholdet \(1:50\).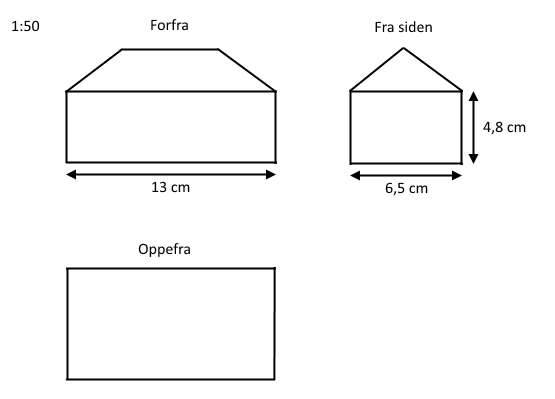

Opgaven lyder på udregne bygningens virkelige højde samt væggene i bygningens samlede længde. 

Højde:
Ud fra den tekniske tegnning kan vi se, at højden på bygningen er 4,8 cm. Da vi skal finde ud af hvor meget dette svarer til i virkeligheden skal vi gange med målestoksforholdet 50. Altså:
$$4,8 \mathrm{cm} \cdot 50 = 240 \mathrm{cm} = 2,4 \mathrm{m} $$

Bygningens højde er altså 2,4 m i virkeligheden. 

Længde af vægge:
Ud fra tegningen af bygningen set oppefra kan vi se at bygningen består af to vægge, der udgør 13 cm på tegningen samt to vægge, der udgør 6,5 cm på tegningen. Udregner vi hvad hver væg svarer til i virkeligheden får vi:
Længste væg: \(13 \mathrm{cm} \cdot 50 = 650 \mathrm{cm} = 6,5 \mathrm{m} \)
Korteste væg: \(6,5 \mathrm{cm} \cdot 50 = 325\mathrm{cm} = 3,25 \mathrm{m} \)

Da vi har to af hver væg bliver den samlede længde af væggene:
$$(2 \cdot 6,5 \mathrm{m}) + (2 \cdot 3,25 \mathrm{m}) = 19,5 \mathrm{m}$$
Dvs, at den samlede længde af væggene til bygningen altså er 19,5 m i virkeligheden.