Areal

I dette afsnit vil vi gennemgå, hvordan man beregner arealet af forskellige geometriske figurer. Vi starter med rektanglet og bevæger os derefter videre til andre figurer. For hver af dem giver vi et argument for, hvorfor arealformlen ser ud, som den gør.

Rektanglet

Et rektangel er en firkant, hvor alle vinkler er 90º.

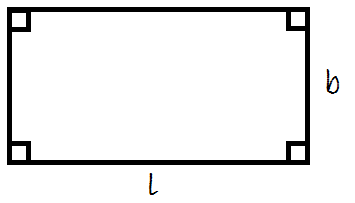
Man finder arealet ved at gange længden med bredden.

$$A=l\cdot b$$

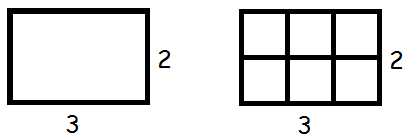
Et eksempel på dette er, at et rektangel med længde 3 og bredde 2 har areal 6. Dette fremgår af denne tegning

Retvinklet trekant

Når vi har med trekanter at gøre, så betegnes arealet ofte med T.

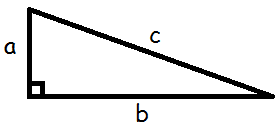
Vi finder arealet af en retvinklet trekant ved at gange de to kateter med hinanden og dividere med to.

$$T=\frac{1}{2}\cdot a\cdot b$$

Læg mærke til, at hvis vi kalder b for grundlinjen, så er a højden til b. Derfor kan vi også skrive formlen

$$T=\frac{1}{2}\cdot \text{højde}\cdot \text{grundlinje}$$

$$T=\frac{1}{2}\cdot h\cdot g$$

Lad os prøve at se på, hvorfor formlen ser ud, som den gør. Hvis vi "kopierer" vores retvinklede trekant, vender kopien på hovedet og sætter den fast ovenpå den originale, så har vi et rektangel.

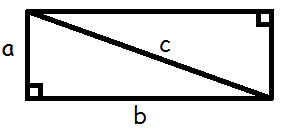
Arealet af to retvinklede trekanter er altså det samme som arealet af et rektangel (længde gange bredde)

$$2T=a\cdot b$$

Vi ganger med en halv på begge sider af lighedstegnet

$$ \frac{1}{\not2}\cdot\not2\cdot T=\frac{1}{2}\cdot a\cdot b$$

$$T=\frac{1}{2}\cdot a\cdot b$$

og så nåede vi frem til formlen.

Trekant

Hvis vi har at gøre med en vilkårlig trekant, så er formlen for arealet den samme

$$T=\frac{1}{2}\cdot h\cdot g$$

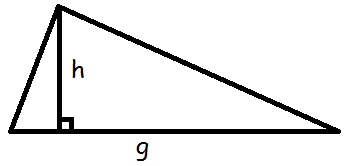
Grunden til at formlen ser sådan ud skyldes, at højden deler trekanten i to retvinklede trekanter.

Vi ved ikke hvor store dele grundlinjen bliver delt i, men hvis vi kalder den lille del for x, så må den store del være resten af grundlinjen (altså grundlinjen foruden x (g-x)).

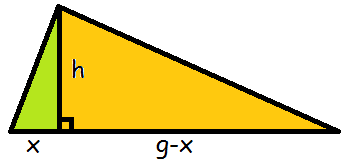
Arealet af trekanten må være arealet af den grønne trekant + arealet af den orange trekant. Den grønne trekant har kateterne x og h, derfor bliver arealet

$$T_\text{grøn}=\frac{1}{2}\cdot h\cdot x$$

Den orange trekant har kateterne h og (g-x), derfor må arealet være

$$T_\text{orange}=\frac{1}{2}\cdot h\cdot (g-x)=\frac{1}{2}\cdot h\cdot g-\frac{1}{2}\cdot h\cdot x$$

Når vi lægger dem sammen, får vi arealet af hele trekanten.

$$T=\underbrace{\frac{1}{2}\cdot h\cdot x}_{T_\text{grøn}}+\underbrace{\frac{1}{2}\cdot h\cdot g-\frac{1}{2}\cdot h\cdot x}_{T_\text{orange}}=\frac{1}{2}\cdot h\cdot g$$

Og sådan er man nået frem til arealformlen.

Parallellogram

Et parallelogram er en firkant, hvor siderne er parvist parallelle.

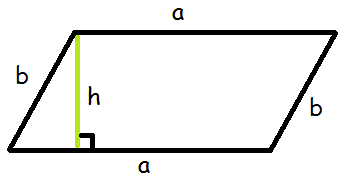
Man finder arealet af parallelogrammet ved at gange højden med grundlinjen.

$$A=\text{højde}\cdot \text{grundlinje} \\A=h\cdot a$$

Grunden til, at formlen ser sådan her ud, er, at hvis man rykker den blå retvinklede trekant fra venstre hen til højre, så har man en rektangel, der har arealet længde gange bredde, altså a gange h.

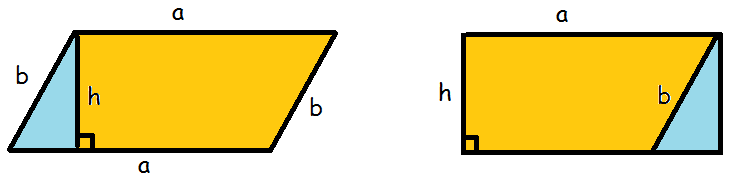
Trapez

Et trapez er en firkant, hvor to af siderne er parallelle. De parallelle sider kalder vi a₁ og a₂. De øvrige sider kunne man have kaldt b og c, men de er ligegyldige, når vi skal finde arealet.

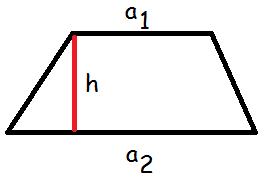
Arealet af et trapez er givet ved formlen:

$$A=\frac{1}{2}\cdot h\cdot (a_1+a_2)$$

Man lægger altså de to parallelle sider sammen, ganger med højden og dividerer med to.

Lad os nu se, hvorfor den formel ser ud som den gør. Vi kan inddele trapezet i to trekanter.

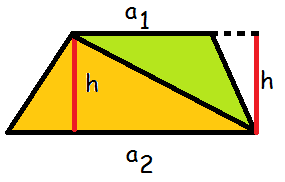
Den orange trekant har grundlinje a₂ og højde h, mens den grønne har grundlinje a₁ og højde h.

Altså er deres arealer

$$T_\text{grøn}=\frac{1}{2}\cdot h\cdot a_1$$

$$T_\text{orange}=\frac{1}{2}\cdot h\cdot a_2$$

Trapezets areal må være summen af de to trekanters areal.

$$A_{trapez}=\frac{1}{2}\cdot h\cdot a_1+\frac{1}{2}\cdot h\cdot a_2$$

Nu sætter vi ½h uden for parentes.

$$A_{trapez}=\frac{1}{2}\cdot h\cdot (a_1+a_2)$$

Og sådan nåede vi frem til den formel.

Cirkel

Den sidste figur, vi skal se på, er cirklen.

Man finder arealet af en cirkel ved at gange π med radius i anden.

$$A=\pi\cdot r^2$$

Den her formel er lidt sværere at forklare. Lad os prøve at inddele cirklen i mange små stykker,klippe dem ud, og omforme dem som på figuren nedenfor

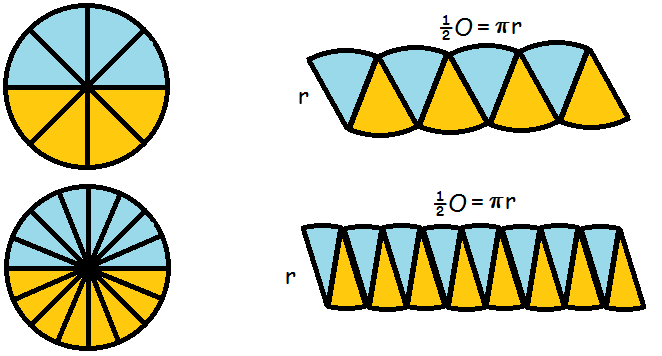
Jo flere stykker, vi har inddelt cirklen i, des mere kommer det til at ligne et rektangel. Hver af stykkerne har sidelængde r, så rektanglets bredde bliver r.
Rektanglets længde består af en masse små buer. De svarer i alt til halvdelen af cirklens omkreds. Vi husker på, at en cirkels omkreds er 2πr

$$A=l\cdot b=\frac{1}{2}O\cdot r=\frac{1}{2}(2\cdot\pi\cdot r)\cdot r=\pi\cdot r\cdot r=\pi\cdot r^2$$

Videolektion