Numeriske ligninger
Numerisk værdi
Når man arbejder med numeriske ligninger, bliver man nødt til at vide, hvad den "numeriske værdi af et tal" betyder. Lad os betragte den reelle tal linje:
![]()
Tallene går fra \(- \infty\) til \(+\infty\), og 0 skiller de positive og negative tal fra hinanden. Den numeriske værdi af et tal er lig med tallets afstand fra 0. Sagt med andre ord: Den numeriske værdi af et tal er altid selve tallet selv med positivt fortegn.
Eksempler:
- Den numeriske værdi af tallet \(-4\) er \(4\)
- Den numeriske værdi af tallet \(-10\) er \(10\)
- Den numeriske værdi af tallet \(5\) er \(5\)
I stedet for at skrive "den numeriske værdi af tallet -4" kan man skrive "\(|-4|\)" - det to lodrette streger betyder "den numeriske værdi af".
Vi kan derfor skrive \(|-4| = 4\), \(|-10| = 10\) og \(|5| = 5\)
Lad os generalisere disse eksempler til en vilkårlig størrelse \(x\) og definere den numeriske værdi:
Lad \(x\) være et reelt tal. Da vil den numeriske værdi af tallet \(x\) være defineret ud fra følgende:
$$
|x| = \begin{cases} \phantom{-}x, & \mathrm{når} \; x\geq0 \; \mathrm{og} \\ -x, & \mathrm{når} \; x<0 . \end{cases}
$$
Denne definition skal forstås (og læses) på følgende måde:
Den numeriske værdi af \(x\) er lig med \(x\) hvis \(x\) er større end, eller lig med 0. Hvis derimod at \(x\) er mindre end 0 så er den numeriske værdi af \(x\) lig med \({-x}\).
I eksemplet ovenfor udnyttede vi denne definition: 5 er eksempelvis større end 0, så den numeriske værdi af 5 er 5. -10 er mindre end 0, så den numeriske værdi af -10 er 10.
Numeriske ligninger
Løser man en ligning, hvor der indgår en numerisk værdi, bliver man nødt til at bruge denne definition. Når vi skal til at løse numeriske ligninger er vi nemlig nødt til at afgøre, hvilke værdier der er tilladte for \(x\) at antage. Dette interval af tilladte værdier for \(x\) kaldes senere hen for definitionsmængden for \(x\). I modsætning til almindelige ligninger, kan numeriske ligninger have mere end 1 løsning. Lad os tage udgangspunkt i et par eksempler.
Eksempel 1
Vi ønsker at løse ligningen
$$
|7-x| = 4x+11,
$$
men før vi kan gå videre skal vi som sagt have fundet ud af hvilke værdier vores \(x\) kan antage for de to forskellige tilfælde, altså for hhv. \(7-x\geq0\) samt \(7-x<0\). Vi ser at
$$
|7-x| = \begin{cases} 7-x, & \mathrm{når} \; 7-x \geq 0 \Rightarrow 7\geq x \\ -(7-x), & \mathrm{når} \; 7-x < 0 \Rightarrow 7<x. \end{cases}
$$
Nu har vi fundet ud af, at hvis 7 er større end, eller lig med \(x\) (eller at \(x\) er mindre end, eller lig med 7), så kan vi helt fjerne det numeriske tegn og bare skrive \(7-x\) på venstresiden. Hvis derimod at \(x\) er større end 7 så skal vi skrive \(-(7-x)\) på venstresiden. Vi har altså nu to ligninger vi kan løse for \(x\).
Lad os starte med at antage at 7 \(\geq x\). Vores ligning kan så skrives som
$$\begin{align}
7-x & = 4x+11 \Leftrightarrow\\
-4 & = 5x \Leftrightarrow\\
x & = -\frac{4}{5} = -0,\!8 .
\end{align}$$
Hvis vi derimod antager at \(x >\) 7 kan vores ligning skrives som
$$\begin{align}
-(7-x) & = 4x+11 \Leftrightarrow\\
-7+x & = 4x+11 \Leftrightarrow\\
-18 & = 3x \Leftrightarrow\\
x & = -\frac{18}{3} = -6.
\end{align}$$
Lad os nu se på de to løsninger og se om en, eller begge, opfylder vores antagelse om hvilke værdier \(x\) kan antage. Hvis vi ser på den sidste løsning først, så antog vi at \(x\) var skarpt større end 7, men da vi løste ligningen så skulle \(x\) være -6 for at den var opfyldt. Da -6 ikke er større end 7 er dette ikke en gyldig løsning.
\(\hspace{10pt}\)Kigger vi derimod på den første løsning, så antog vi at \(x\) var mindre end, eller lig med 7, og da vi løste ligningen fandt vi at \(x\) skulle være -0,8 for at den var opfyldt. Da -0,8 er mindre end 7 er denne løsning gyldig og dermed kan vi konkludere at løsningen til vores numeriske ligning
$$
|7-x| = 4x+11,
$$
er \(x =\) -0,8.
Eksempel 2
Lad os tage endnu et eksempel. Denne gang skal vi løse ligningen
$$
|2x-13| = |{-2}-x|.
$$
Igen skal vi have fundet ud af, hvilke intervaller \(x\) skal ligge i, men hvor vi før kun gjorde det for den ene side, og fik to intervaller, skal vi nu gøre det for begge sider, hvilket vil give os tre intervaller for \(x\). Lad os starte med venstresiden
$$
|2x-13| = \begin{cases} 2x-13, & \mathrm{når} \; 2x-13 \geq 0 \Rightarrow x \geq 6,\!5 \\ -(2x-13), & \mathrm{når} \; 2x-13 < 0 \Rightarrow x < 6,\!5 \end{cases}
$$
og så højresiden
$$
|{-2}-x| = \begin{cases} {-2}-x, & \mathrm{når} \; {-2}-x \geq 0 \Rightarrow -2\geq x \\ -({-2}-x), & \mathrm{når} \; {-2}-x < 0 \Rightarrow -2<x. \end{cases}
$$
Fra venstresiden fandt vi, at \(x\) enten skulle være større end eller lig med 6,5, eller mindre end 6,5. Fra højresiden fandt vi derimod at \(x\) enten skulle være mindre end eller lig med -2, eller større end -2. Dette kan vi omformulere til tre intervaller for \(x\).
\(\hspace{10pt}\)I det første interval kræver vi at \(x\) er mindre end, eller lig med -2.
\(\hspace{10pt}\)I det næste interval skal \(x\) både være større end -2 og samtidig mindre end 6,5. Dette skrives \(-2<x<6,\!5\).
\(\hspace{10pt}\)Det sidste interval kræver at \(x\) er større end eller lig med 6,5. Som før kan vi nu løse ligningen i disse tre tilfælde.
Først antager vi at \(x\leq-2\), hvilket gør at vi kan skrive ligningen som
$$\begin{align}
-(2x-13) & = -2-x \Leftrightarrow\\
-2x+13 & = -2-x \Leftrightarrow\\
15 & = x .
\end{align}$$
Så antager vi at \(-2<x<6,\!5\), hvorved vi kan skrive
$$\begin{align}
-(2x-13) & = -(-2-x) \Leftrightarrow\\
-2x+13 & = 2 + x \Leftrightarrow\\
11 & = 3x \Leftrightarrow\\
x & = \frac{11}{3} \approx 3,\!67 .
\end{align}$$
Til sidst antager vi at \(x\geq6,\!5\)
$$\begin{align}
2x-13 & = -(-2-x) \Leftrightarrow\\
2x-13 & = 2+x \Leftrightarrow\\
x & = 15 .
\end{align}$$
Lad os nu se på om løsningerne opfylder de krav vi har for de værdier \(x\) kan antage.
\(\hspace{10pt}\)I det første tilfælde krævede vi at \(x\leq-2\) hvilket gav os løsningen \(x=15\). Da 15 tydeligvis ikke er mindre end eller lig med -2 er denne løsning ikke gyldig.
\(\hspace{10pt}\)I det andet tilfælde krævede vi at \(-2<x<6,\!5\) hvilket gav os løsningen \(x\approx3,\!67\). Da 3,67 er større end -2 og mindre end 6,5 er dette en gyldig løsning.
\(\hspace{10pt}\)I sidste tilfælde krævede vi at \(x\geq6,\!5\) og fandt løsningen \(x=15\). Da 15 er større end 6,5 er dette også en gyldig løsning og vi kan dermed konkludere at løsningen til ligningen
$$
|2x-13| = |{-2}-x|
$$
er \(x \approx 3,\!67\) eller \(x= 15\). Dette kan også skrives mere matematisk korrekt som \(x \approx 3,\!67 \vee x = 15\).
Eksempel 3
Vi vil løse ligningen \(|x+3| = |20 - 4x|\):
Først bestemmes intervallerne for hhv. \(|x+3|\) og \(|20 - 4x|\):
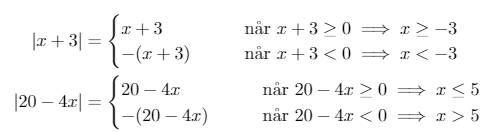
Herved får vi fire forskellige intervaller: \( x<-3\), \(x \geq -3\), \(x \leq 5\) og \(x>5\).
Hvis intervallerne tegnes, ses det, at der i realiteten kun er tale om tre intervaller:
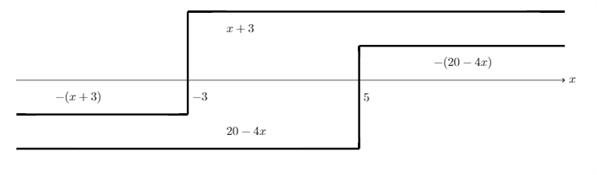
- Det første interval er \(x<-3\), og det løses: \(-(x+3)=20-4x \implies x=7,67\). Denne løsning ligger uden for intervallet, hvorfor denne løsning kasseres.
- Det andet interval er \(-3 \leq x \leq 5\). Dette løses på denne måde: \(x+3=20-4x \implies x=3,4\). Denne løsning ligger inden for intervallet, så den forkastes ikke.
- Det tredje interval er \(x>5\). Det løses på denne måde: \(x+3 = -(20-4x) \implies x=7,67\) Denne løsning ligger nu inden for intervallet, så den forkastes ikke.
