Tangens

Tangens er en trigonometrisk funktion ligesom cosinus og sinus. Det er ligeledes en funktion, hvor man kommer en vinkel ind, men i modsætning til cosinus og sinus, hvor man kun kunne få et tal ud mellem -1 og 1, så kan man få alle reelle tal ud med tangens.

Tangens er defineret til at være

$$\tan(v)=\frac{\sin(v)}{\cos(v)}$$

Som et eksempel kan man beregne tangens til en vinkel på 35 grader således

$$\tan(35)=\frac{\sin(35)}{\cos(35)}=\frac{0,574}{0,819}=0,700$$

Bemærk, at mens man må komme alle vinkler ind i cosinus og sinus, så er der nogle forbudte værdier for tangens. Tangens er nemlig defineret som en brøk, og i en brøk må nævneren aldrig give 0. Så de vinkler, der gør at nævneren (cos(v)) giver 0, er forbudte.

Ved at se på enhedscirklen kan man indse, at de vinkler, der giver cos(v)=0 er

$$90^\circ,\: 270^\circ,\: 450^\circ,\:630^\circ.\,.\,.$$

hvor man lægger 180 til hver gang.

Ligesom cosinus og sinus kunne visualiseres ved hjælp af enhedscirklen, så kan tangens også aflæses på en sådan tegning. Man starter med at indtegne linjen x=1, altså en lodret linje, der tangerer enhedscirklen i punktet (1, 0). Så ser man på, hvor venstre vinkelben skærer denne linje. Skæringspunktets y-koordinat er
tangens til vinklen.

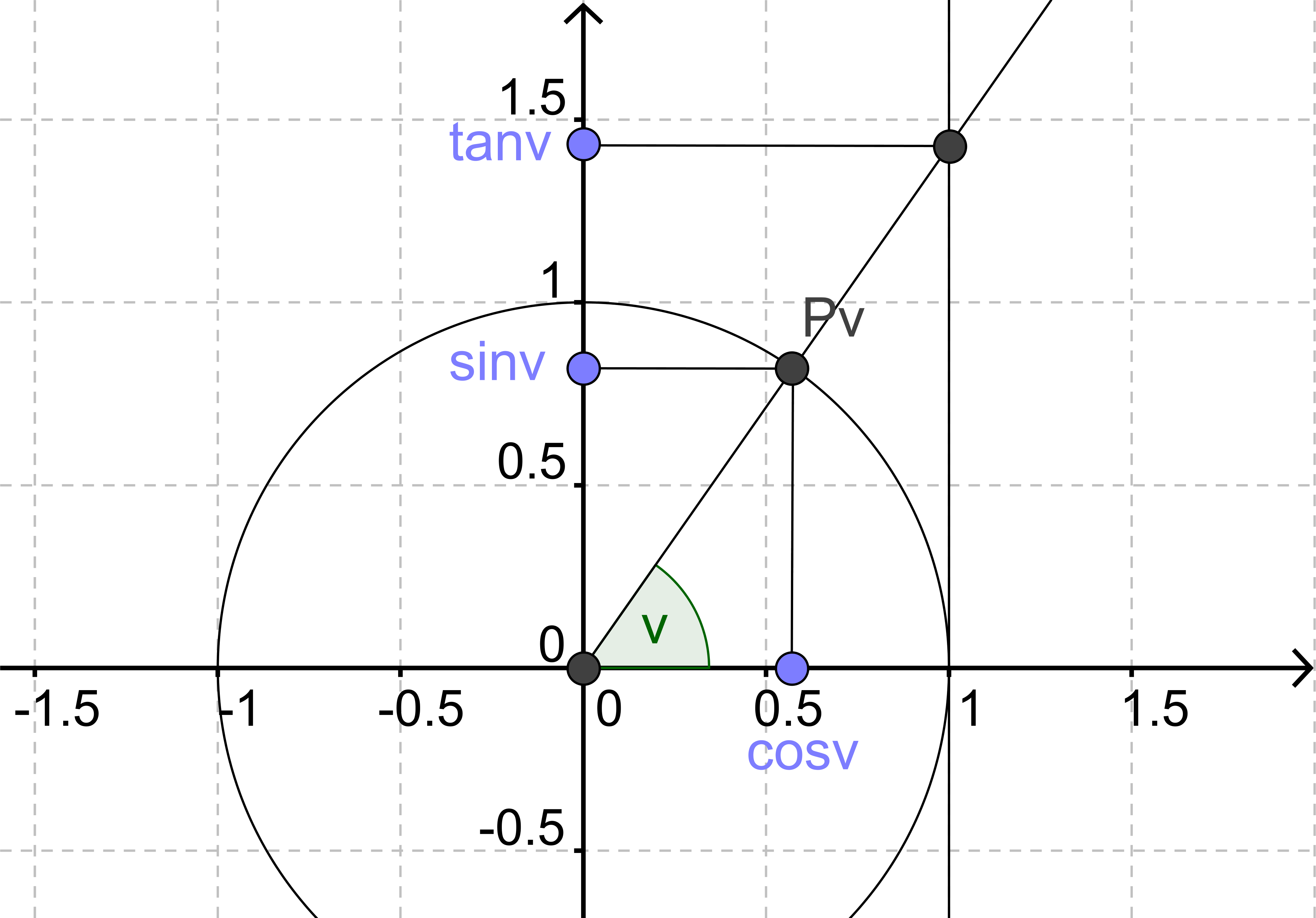
Det er ikke umiddelbart klart, hvorfor det forholder sig sådan. Tricket til at gennemskue det er, at den blå og den røde trekant på tegningen nedenfor er ensvinklede

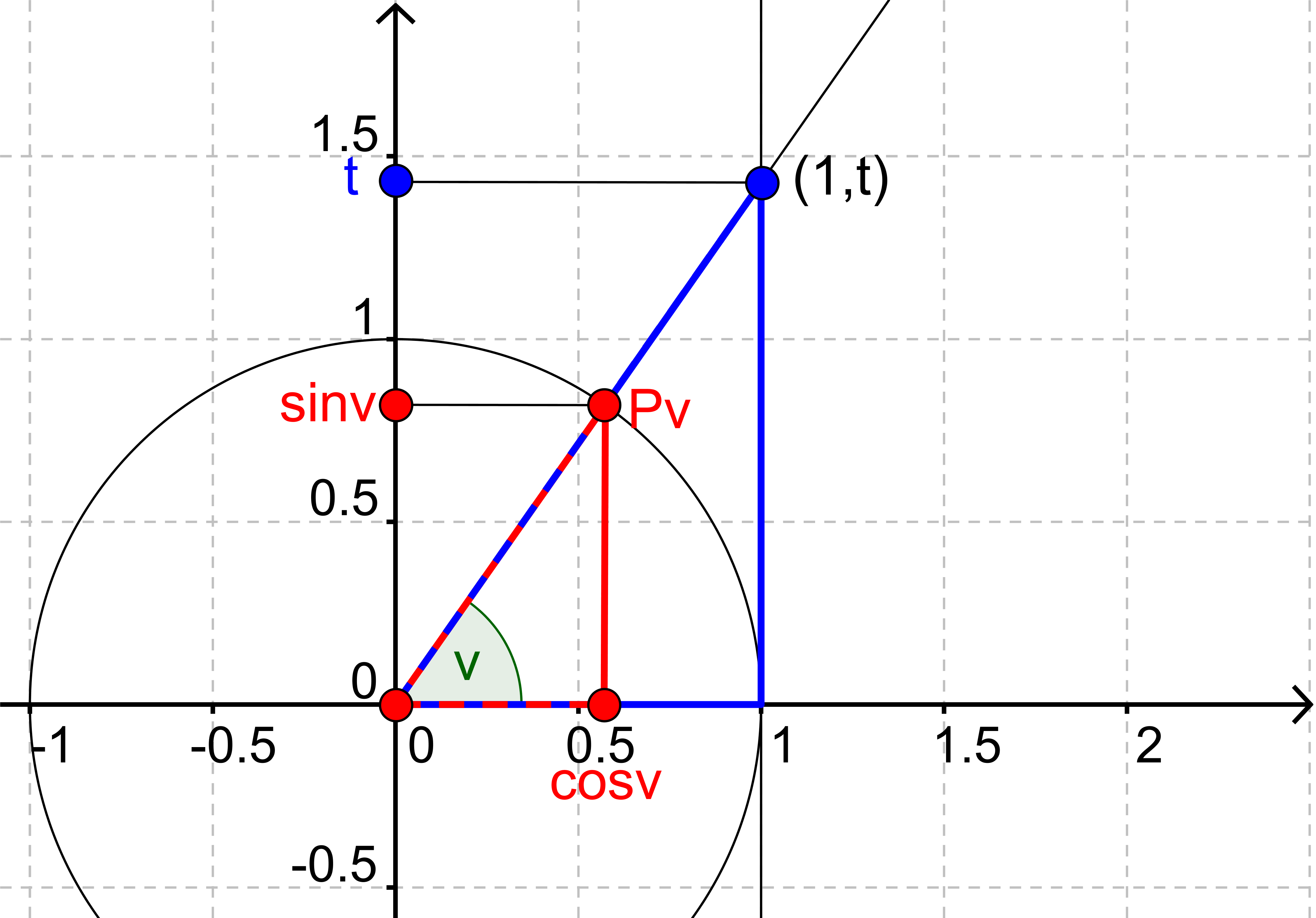
Vi vil gerne vise, at det, der hedder "t" på tegningen, er det samme som tangens til v.

Vi ser, at cos(v) i den røde trekant er ensliggende med 1 i den blå, og at sin(v) i den røde trekant er ensliggende med t i den blå.

Da den røde og den blå trekant er ensvinklede, er forholdet mellem to sider i den røde trekant det samme som forholdet mellem de to ensliggende sider i den blå trekant.

Altså har vi

$$\frac{\sin(v)}{\cos(v)}=\frac{t}{1}=t$$

men vi har også at

$$\tan(v)=\frac{\sin(v)}{\cos(v)}$$

og derfor er

$$\tan(v)=t$$

---

Videolektion