Addition og subtraktion af brøker

Som vi nævnte i i afsnittet om brøker, så gælder det, at jo færre dele noget er opdelt i, des større er hver del. Hvis vi vil lægge 1/6 og 1/4 sammen, får vi derfor problemer, da 1'erne ikke repræsenterer en lige stor del.

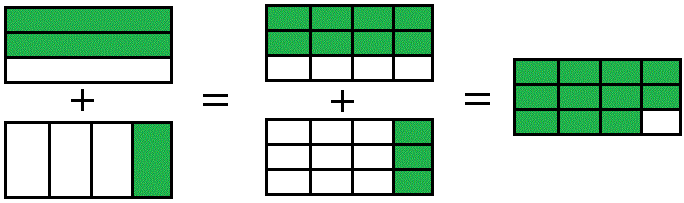
Hvis vi i stedet vil lægge brøker sammen, der har den samme nævner, så går det lettere, da nævnerne har samme størrelse, og delene derfor er sammenlignelige.

$$\frac{1}{5}+\frac{2}{5}=\frac{3}{5}$$

Hvis vi vil lægge to brøker sammen, der har forskellige nævnere, skal vi altså først sørge for at give dem en fælles nævner, før vi kan udføre additionen. Vi bruger teknikkerne at forlænge og forkorte brøker for at opnå en fællesnævner. F.eks.

$$\frac{2}{3}+\frac{1}{4}=\frac{2\cdot4}{3\cdot4}+\frac{1\cdot3}{4\cdot3}=\frac{8}{12}+\frac{3}{12}=\frac{11}{12}$$

Her har vi forlænget brøkerne med hhv. 4 og 3 for at opnå en fællesnævner på 12.

Når vi skal trække to brøker fra hinanden, gælder også, at vi skal have fællesnævner, før vi subtraherer (minusser). F.eks. dette stykke, hvor vi forlænger med hhv. 2 og 7 for at få en fællesnævner på 14.

$$\frac{5}{7}-\frac{1}{2}=\frac{5\cdot2}{7\cdot2}-\frac{1\cdot7}{2\cdot7}=\frac{10}{14}-\frac{7}{14}=\frac{3}{14}$$

Hvis vi skriver med symboler, har vi altså reglerne

$$\begin{align*}\frac{a}{c}+\frac{b}{c}&=\frac{a+b}{c}\\\\\frac{a}{c}-\frac{b}{c}&=\frac{a-b}{c}\end{align*}$$

Bemærk, at når vi adderer og subtraherer brøker, er det kun tællerne vi regner på.

Videolektion