Logaritmer
Hvordan løser vi ligningen
$$10^x=200\:?$$
En måde er at gøre det grafisk
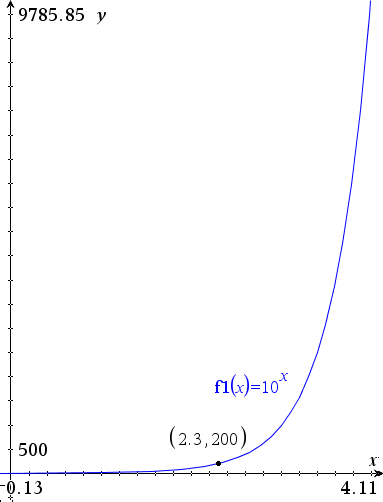
Vi kan altså se, at løsningen til ligningen er x=2,3.
Det ville imidlertid være smart, hvis vi kunne regne det ud uden at være nødt til at aflæse på en graf.
Det er derfor man har opfundet logaritmer.
Den eksponent, man skal opløfte 10 til for at få 200 kaldes 10tals-logaritmen til 200
Vi siger
$$\log_{10}(200)=2,3 \quad \text{fordi} \quad 200=10^{2,3}$$
Vi kan gøre det mere generelt:
$$\text{Hvis} \quad y=10^x\quad \text{ så er} \quad\log_{10}(y)=x$$
eller sagt på en anden måde
$$\log_{10}(10^x)=x$$
Med ord ville man sige
10tals-logaritmen til et positivt tal er den eksponent, 10 skal opløftes til for at give tallet.
Her er nogle eksempler på, hvordan vi finder logaritmen til nogle tal.
$$\log_{10}(1000)=3\quad fordi\quad 10^3=1000$$
$$\log_{10}(100)=2\quad fordi\quad 10^2=100$$
$$\log_{10}(10)=1\quad fordi\quad 10^1=10$$
$$\log_{10}(1)=0 \quad fordi\quad 10^{0}=1$$
$$\log_{10}(0,1)=-1\quad fordi\quad 10^{-1}=0,1$$
$$\log_{10}(0,01)=-2\quad fordi\quad 10^{-2}=0,01$$
Og her ser vi, hvordan vi finder 10tals-logaritmen til de første par naturlige tal.
$$\log_{10}(1)=0\quad fordi\quad 10^0=1$$
$$\log_{10}(2)=0,301\quad fordi\quad 10^{0,301}=2$$
$$\log_{10}(3)=0,477\quad fordi\quad 10^{0,477}=3$$
$$\log_{10}(4)=0,602\quad fordi\quad 10^{0,602}=4$$
$$\log_{10}(5)=0,699\quad fordi\quad 10^{0,699}=5$$
$$\log_{10}(6)=0,778\quad fordi\quad 10^{0,778}=6$$
Ligesom vi så at
$$\log_{10}(10^x)=x$$
kan vi også vende det om og se at
$$10^{\log_{10}(x)}=x$$
Logaritmeregneregler
Når vi regner med logaritmer, er der nogle vigtige regneregler.
$$1.\quad\log(a\cdot b)=\log(a)+\log(b)$$
$$2.\quad\log\left(\frac{a}{b}\right)=\log(a)-\log(b)$$
$$3.\quad\log(a^x)=x\cdot\log(a)$$
Med ord kan vi sige
- logaritmer oversætter gange til plus
- logaritmer oversætter dividere til minus
- når man tager logaritmen til en potens, må man rykke eksponenten ned foran.
Man kan bruge reglerne til at omforme udtryk, så de bliver lettere at regne ud. Lad os tage nogle eksempler
Hvis vi ønsker at udregne
$$\log_{10}(30)$$
kan vi benytte 1. regel
$$\log_{10}(30)=\log_{10}(6\cdot5)\stackrel{1.}{=}\log_{10}(6)+\log_{10}(5)=0,778+0,699=1,477$$
Hvis vi ønsker at beregne
$$\log_{10}(0,9)$$
kan vi benytte regel 2 og regel 3, på følgende måde
$$\log_{10}(0,9)=\log_{10}(\frac{9}{10})\stackrel{2.}{=}\log_{10}(9)-\log_{10}(10)=\log_{10}(3^2)-\log_{10}(10)$$
$$\stackrel{3.}{=}2\cdot\log_{10}(3)-\log_{10}(10)=2\cdot 0,477-1=-0,046$$
I afsnittet om potensfunktioner, skulle vi udregne
$$\frac{\log_{10}(36)-\log_{10}(4)}{\log_{10}(3)-\log_{10}(1)}$$
Umiddelbart ser det svært ud, men ved at bruge reglerne ovenfor kan vi udregne det uden brug af lommeregner.
$$\frac{\log_{10}(36)-\log_{10}(4)}{\log_{10}(3)-\log_{10}(1)}\stackrel{2.}{=}\frac{\log_{10}(\frac{36}{4})}{\log_{10}(\frac{3}{1})}=\frac{\log_{10}(3^2)}{\log_{10}(3)}\stackrel{3.}{=}\frac{2\cdot\log_{10}(3)}{\log_{10}(3)}=2$$
Nu har vi set eksempler på, hvordan vi kan bruge logaritmeregnereglerne. Men hvorfor virker de egentlig? Det spørgsmål besvarer vi her ved at forklare reglerne.
For at forstå den første logaritmeregneregel skal vi huske på tre ting.
$$\log_{10}(10^x)=x\\10^{\log_{10}(x)}=x$$
samt potensregnereglen:
$$a^x\cdot a^y=a^{x+y}$$
Nu er vi klar til at forklare den første logaritmeregneregel.
$$\log_{10}(a\cdot b)=\log_{10}(10^{\log_{10}(a)}\cdot10^{\log_{10}(b)})\\=\log_{10}(10^{\log_{10}(a)+\log_{10}(b)})=\log_{10}(a)+\log_{10}(b)$$
På samme måde kan vi forklare 2. logaritmeregneregel
$$\log_{10}(\frac{a}{b})=\log_{10}(\frac{10^{\log_{10}(a)}}{10^{\log_{10}(b)}})\\=\log_{10}(10^{\log_{10}(a)-\log_{10}(b)})=\log_{10}(a)-\log_{10}(b)$$
Til at forklare den tredje regneregel, skal vi benytte den første.
$$\log_{10}(a^x)=\log_{10}(\underbrace{a\cdot.\,.\,.\cdot a}_{x\,gange})\stackrel{1.}{=}\underbrace{\log_{10}(a)+.\,.\,.+\log_{10}(a)}_{x\,gange}=x\cdot\log_{10}(a)$$
Den naturlige logaritme og andre logaritmer
Den almindelige logaritme kaldes ofte for 10tals-logaritmen. Dette skyldes, at man jo skal se, hvilken eksponent man skal opløfte 10 til for at få tallet. Vi siger, at 10 er grundtallet. Men man kan også forestille sig logaritmer med andre grundtal.
En af de mest anvendte er Den Naturlige Logaritme. Denne betegnes ofte med \(\ln{(x)}\). Grundtallet i den naturlige logaritme er Eulers tal.
$$e\approx2,71828$$
For den naturlige logaritme gælder altså
$$\text{Hvis}\quad y=e^x\quad \text{så er}\quad \ln(y)=x$$
eller sagt på en anden måde
$$\ln(e^x)=x $$
$$e^{\ln(x)}=x$$
Man kan også bruge andre grundtal end 10 og e. I alle tilfælde markerer man hvilket grundtal man bruger ved at skrive det med sænket skrift efter log. F.eks. ville man skrive 2tals-logaritmen således:
$$\text{Hvis}\quad y=2^x\quad \text{så er}\quad\log_2(y)=x$$
Man kan gøre det helt generelt med at skrive
$$y=a^x\Leftrightarrow \log_a(y)=x$$
BEMÆRK:
logaritmeregnereglerne gælder for alle logaritmer uanset grundtallet!
$$1.\quad\log_a(x\cdot y)=\log_a(x)+\log_a(y)$$
$$2.\quad\log_a\left(\frac{x}{y}\right)=\log_a(x)-\log_a(y)$$
$$3.\quad\log_a(x^y)=y\cdot\log_a(x)$$
