Trekanter og vinkler
Trekanter og udregninger af sider og vinkler har udgjort en vigtig del af geometrien gennem flere tusinde år.
I dette afsnit skal vi prøve at få styr på nogle af de grundlæggende ting ved trekanterne.
Når vi med symboler skal omtale en trekant, så tegner vi først en lille trekant Δ, hvorefter vi skriver navnene på de tre hjørner i trekanten. F.eks. ville man skrive
$$\triangle ABC $$
for at benævne denne trekant
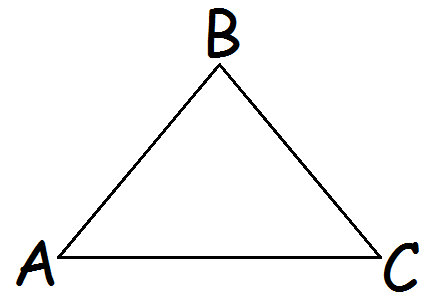
Det er smart at skrive det på den måde for at kunne skelne to trekanter fra hinanden.
Vi plejer at betegne hjørnerne i en trekant med store bogstaver, og de overfor liggende sider med små bogstaver
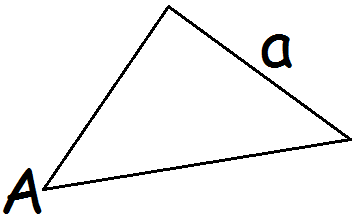
Vinklerne i en trekant plejer vi at betegne med et vinkeltegn efterfulgt af hjørnets bogstav. F.eks.
$$\angle A$$
Nogle gange kan der imidlertid være flere vinkler fra samme hjørne. For at markere hvilken vinkel, man så taler om, kan man efter vinkeltegnet skrive højre vinkelbens endepunkt, hjørnet vinklen er i, og venstre vinkelbens endepunkt.
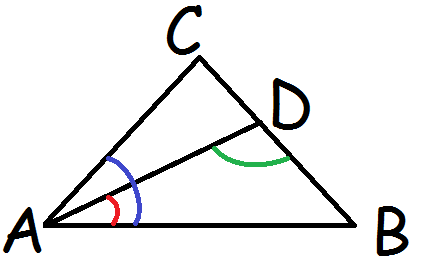
Her vil den blå vinkel hedde
$$\angle BAC$$
mens den røde vinkel vil hedde
$$\angle BAD$$
og den grønne vil hedde
$$\angle ADB$$
Spidsvinklede og stumpvinklede trekanter
En trekant er spidsvinklet, hvis alle vinklerne i den er spidse (det vil sige under 90º)
Hvis en af vinklerne er stump (større end 90º), kaldes trekanten stumpvinklet.
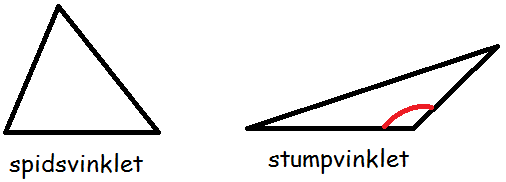
Vinkelsum
Vinkelsummen i en trekant vil altid være 180 grader. Argumentet for at det er sådan fat er følgende tegning.
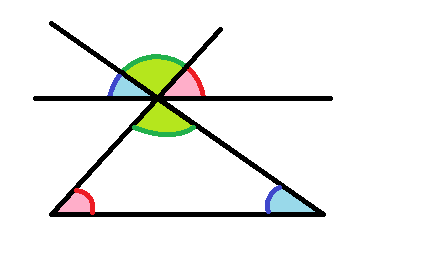
Det er tydeligt, at de tre vinkler foroven udgør 180º. Den blå vinkel foroven er tydeligvis lige så stor som den blå vinkel i trekanten, fordi de er tegnet ud fra to parallelle linjer. På samme måde er de to røde vinkler lige store. Det er ikke lige så klart, at de to grønne vinkler er ens, men det er de, fordi de er topvinkler (hvilket vi kommer tilbage til nedenfor). Altså har vi at de tre vinkler i trekanten er ens med de tre vinkler foroven, der tilsammen udgør 180º. Derfor må de tre vinkler i trekanten sammenlagt være 180º.
Topvinkler
Når man har at gøre med to rette linjer, der skærer hinanden, kan man tale om topvinkler. Topvinkler er sådan nogle som v og w på tegningen herunder. Der gælder, at topvinkler er lige store.
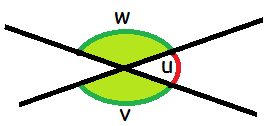
Vi kan se, at
$$u+v=180^\circ$$
og at
$$u+w=180^\circ$$
Hvis vi isolerer v i den første ligning og w i den næste får vi
$$v=180^\circ-u$$
$$w=180^\circ-u$$
Altså er v og w lig med det samme, og derfor er de ens.
