Volumen og overfladeareal
I dette afsnit skal vi se lidt nærmere på volumen/rumfang. Hvor arealet målte noget 2 dimensionalt, så er volumen et 3dimensionalt mål. Man kan sige, at areal er et flademål, og volumen et rummål.
At bestemme volumen er det samme som at finde ud af, hvor meget der kan være inde i figuren. Når vi har at gøre med 3dimensionale figurer, så har de jo en overflade, og man kan derved beregne
overfladearealet. I de fleste figurer er det blot at beregne arealet af hver af siderne, men i nogle er det mere kompliceret.
Kasse
En kasse, der er sammensat af rektangler (dvs. alle vinkler er 90 grader) er let at beregne volumen af. Man ganger simpelthen bare længde, bredde og højde med hinanden.
$$V=l\cdot b\cdot h$$
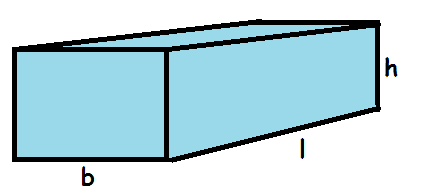
Man kunne også forestille sig en kasse, hvor endestykkerne er parallelogrammer
I så fald skal man finde arealet af grundfladen og gange med figurens højde.
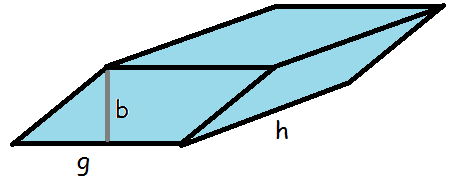
Her skal man holde tungen lige i munden. Der er nemlig dels kassens højde (markeret med h) og så er der højden i parallelogrammet, der markeres med b for at kende forskel. Parallelogrammets areal er højde gange grundlinje.
Vi udregner altså volumen således:
$$V=\text{grundflade}\cdot \text{højde} $$
$$V= b\cdot g\cdot h$$
Hvis vi havde at gøre med en kasse, hvis grundflade var et trapez, ville vi også skulle gange kassens højde med grundfladens areal for at få volumen.
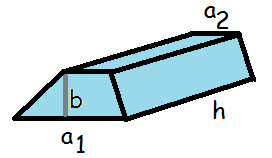
Her er arealet af grundfladen (se areal)
$$A_{grundflade}=\frac{1}{2}\cdot b\cdot(a_1+a_2)$$
Så volumen bliver
$$V=\text{højde}\cdot \text{grundflade}$$
$$V=\frac{1}{2}\cdot b\cdot h\cdot(a_1+a_2)$$
Cylinder
Det er også tit nyttigt at beregne volumen af en cylinder.
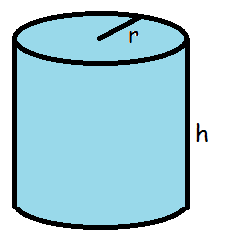
Her skal man gøre præcist som ovenfor. Først skal man finde arealet af grundfladen (cirklen) og dernæst gange det med cylinderens højde.
Fra afsnittet om arealer ved vi, at en cirkels areal er
$$A_{cirkel}=\pi\cdot r^2$$
Nu kan vi finde volumen af cylinderen
$$V_{cylinder}=h\cdot\pi\cdot r^2$$
Vi finder arealet af den krumme overflade, O, ved at gange cirklens omkreds med højden
$$O=2\cdot\pi\cdot r\cdot h$$
Hvis vi vil have det samlede overfladeareal, A, inklusiv top og bund, skal vi lægge arealet af to cirkler til
$$A=2\cdot\pi\cdot r\cdot h+2\cdot\pi\cdot r^2$$
$$A=2\cdot \pi \cdot r\cdot(h+r)$$
Prisme
Prismen har lige som de ovenfor nævnte figurer en højde og en grundflade. Grundfladen er her en trekant.
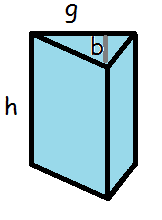
$$V=\text{højde}\cdot \text{grundflade}$$
$$V_{prisme}=\frac{1}{2}\cdot h\cdot b\cdot g$$
Kugler
Ovenfor har vi beskæftiget os med figurer, der har en grundflade. Men ikke alle figurer har det. Tag f.eks. kuglen.
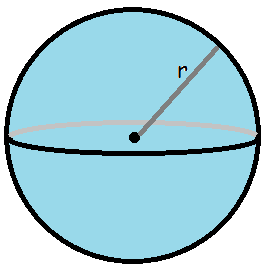
Man beregner kuglens volumen ved hjælp af formlen
$$V_{kugle}=\frac{4}{3}\cdot\pi\cdot r^3$$
og overfladearealet beregner man således:
$$A_{kugle}=4\cdot\pi\cdot r^2$$
Kegle
Volumen af en kegle er præcis en tredjedel af en cylinder med samme radius og højde.
$$V_{kegle}=\frac{\pi\cdot h\cdot r^2}{3}$$
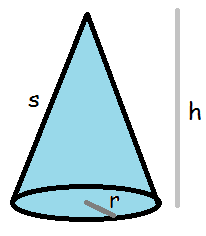
Arealet af den krumme overflade beregnes således
$$O_{kegle}=\pi\cdot r\cdot s$$
Det samlede overfladeareal (inklusiv bunden) er derfor
$$A_{kegle}=\pi\cdot r\cdot s+\pi\cdot r^2 $$
$$A_{kegle}=\pi\cdot r\cdot(s+r)$$
Pyramide
En pyramide er en figur, der har en grundflade, hvor hvert af grundfladens hjørner er forbundet til et punkt, der ligger over grundfladen.
Grundfladen kan eksempelvis være trekantet eller firkantet, som det ses på tegningerne, men kan også have flere kanter (den skal altså være en polygon. Polygon er det græske ord for mangekant).
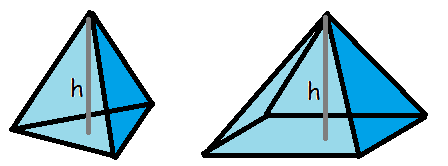
Det forholder sig ligesom med keglen, at rumfanget af en pyramide er en tredjedel af den tilsvarende kasse/prisme. Altså højden gange grundfladens areal divideret med 3.
$$V_{\mathrm{pyramide}}=\frac{\mathrm{A_{\mathrm{grundflade}}}\cdot \mathrm{højde}}{3}$$
Overfladearealet af en pyramide findes ved at lægge grundfladearealet sammen med de trekantede sidefladers samlede areal. Du kan finde arealet af en trekant med $$A_{\mathrm{trekant}}=\frac{1}{2}\cdot h_{\mathrm{trekant}}\cdot g$$Vær opmærksom på de to forskellige højder: Pyramidens højde og trekantens højde.
En regulær polygon er en polygon, hvor alle sider er lige lange.
Hvis en pyramide har en regulær polygon som grundflade, og polygonen har n sider (der alle har længden g), kan overfladearealet A for pyramiden findes ved
$$A_{\mathrm{pyramide}}= A_{\mathrm{grundflade}} + n \cdot \frac{1}{2}\cdot h_{\mathrm{trekant}}\cdot g$$
Hvis pyramiden har en irregulær polygon som grundflade, er man nødt til at udregne arealet af hver trekant for sig og lægge alle disse arealer sammen med arealet af grundfladen.
