Eksponentiel udvikling
Hvis du har at gøre med noget, der vokser/aftager med en fast procent pr. tidsenhed, så er der tale om eksponentiel udvikling. Et vigtigt eksempel på eksponentiel udvikling er renteformlen.
Et andet eksempel kunne være en slags bakterie der fordobles (stiger med 100%) hver time. Hvis vi starter med at have 3 bakterier, vil vi efter en time have
$$3\cdot2=6$$
6 bakterier. Efter to timer vil vi have
$$6\cdot2=12$$
12 bakterier. Efter tre timer vil vi have
$$12\cdot2=24$$
24 bakterier, osv...
Læg mærke til, at vi kan skrive tallene om
$$6=3\cdot2^1$$
$$12=3\cdot2^2$$
$$24=3\cdot2^3$$
Hvis vi kalder antallet af bakterier efter x antal timer for y, så kan vi skrive at
$$y=3\cdot2^x$$
Dette er et eksempel på en eksponentiel udvikling.
Generelt er eksponentielle udviklinger på formen
$$y=b\cdot a^x,\quad a>0$$
Vi har allerede set, at x og y er variable, hvor y-værdien afhænger af, hvilken x-værdi vi propper ind på højre side. y er altså den afhængige og x den uafhængige variabel.
Men hvad er så a og b?
a er en konstant, der kaldes fremskrivningsfaktoren. Den fortæller noget om, hvor mange procent y vokser eller aftager med for hvert x. Hvis y vokser med r procent pr x har vi nemlig at
$$a=1+r$$
hvilket er det samme som at sige
$$r=a-1$$
Hvis vi får at vide, at y vokser med 5 procent for hvert x, så er
$$a=1+r=1+5\%=1+0,05=1,05$$
Og hvis vi får at vide, at y aftager med 7 procent for hvert x, så er
$$a=1+r=1+(-7\%)=1-0,07=0,93$$
Og hvis vi får at vide, at a=1,23, så kan vi finde r således
$$r=a-1=1,23-1=0,23=23\%$$
Generelt kan vi sige, at
Hvis a>1, så er udviklingen voksende
Hvis 0<a<1, så er udviklingen aftagende.
Konstanten b kaldes begyndelsesværdien. Det er den værdi, vi starter med. I eksemplet med bakterierne ovenfor var b=3.
På en graf kan vi aflæse b som skæringen med y-aksen.
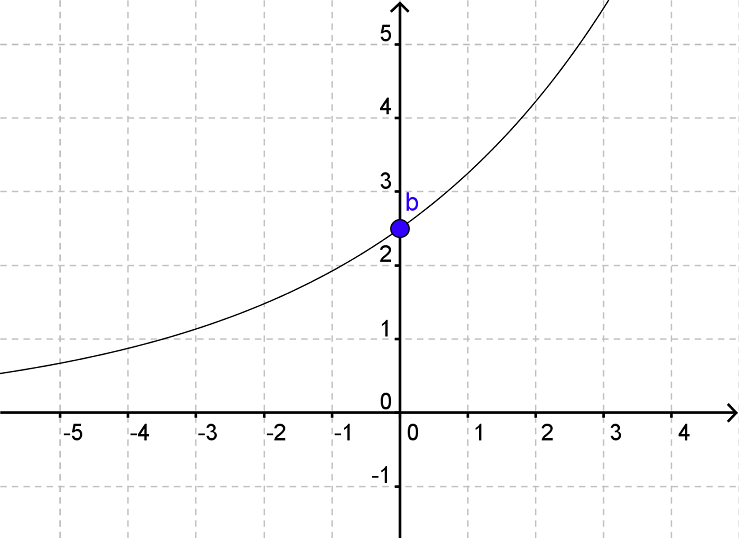
I dette eksempel kan vi se, at b=2,5.
Man kan ikke på samme måde aflæse a ved at se på grafen. Dog kan man se, at hvis a er større end 1, så vil grafen krænge opad, og hvis a er mindre end 1 (men større end nul), så vil grafen krænge nedad.
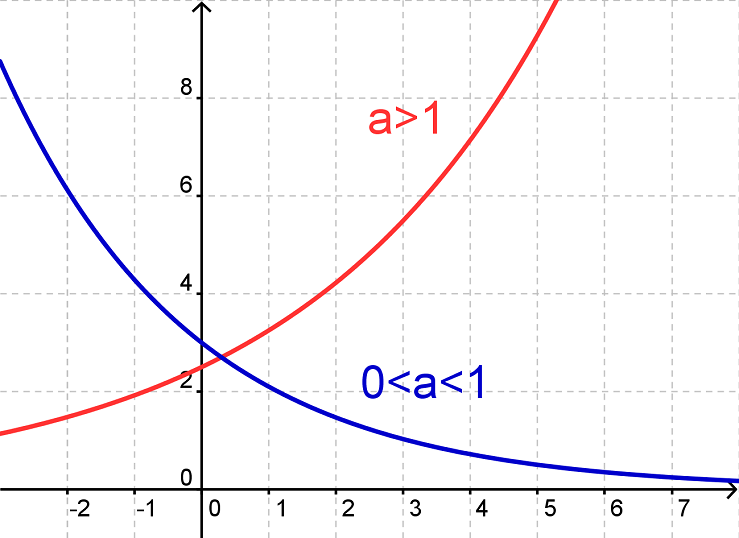
Bemærk, at grafen aldrig krydser x-aksen
Her er en tabel over, hvordan man finder begyndelsesværdi, fremskrivningsfaktor og vækstrate ud fra forskriften for en eksponentiel udvikling.
| Forskrift | Begyndelsesværdi (b) | Fremskrivningsfaktor (a) | Vækstrate/Rentefod (r) | Udvikling |
| \(y=450\cdot1,13^x\) | \(450 \) | \(1,13 \) | \(1,13-1=13\% \) | voksende |
| \(y=217\cdot1,56^x\) | \(217 \) | \(1,56 \) | \(1,56-1=56\% \) | voksende |
| \(y=132\cdot0,81^x\) | \(132 \) | \(0,81 \) | \(0,81-1=-19\% \) | aftagende |
| \(y=1,7\cdot0,1^x\) | \(1,7 \) | \(0,1 \) | \(0,1-1=-90\% \) | aftagende |
| \(y=2,3\cdot5^x\) | \(2,3 \) | \(5 \) | \(5-1=400\% \) | voksende |
Hvis man tegner grafen for en eksponentiel funktion i et enkeltlogaritmisk koordinatsystem (dvs hvor y-skalaen er logaritmisk, og x-skalaen er almindelig), så får man en ret linje.
Find x og y
Når vi kender x og ønsker at finde det tilhørende y, så kan vi bare indsætte x på højresiden og så se, hvilket y, der kommer ud.
Hvis vi derimod kender y og ønsker at finde ud af, hvilket x der hører til, så skal vi først have isoleret x. Til det skal vi bl.a. bruge logaritmeregnereglerne.
$$y=b\cdot a^x$$
$$\frac{y}{b}=a^x$$
$$\log(\frac{y}{b})=\log(a^x)$$
$$\log(y)-\log(b)=x\cdot\log(a)$$
$$\frac{\log(y)-\log(b)}{\log(a)}=x$$
Nu kan vi bestemme x ved formlen
$$x=\frac{\log(y)-\log(b)}{\log(a)}$$
Lad os tage et eksempel.
Hvis vores funktion er
$$y=5\cdot2^x$$
og vi får at vide, at x=3, så kan vi finde y sådan her
$$y=5\cdot2^x=5\cdot2^3=5\cdot8=40$$
Hvis vi derimod får at vide, at y=80, så kan vi bestemme x som
$$x=\frac{\log(y)-\log(b)}{\log(a)}=\frac{\log(80)-\log(5)}{\log(2)}=\frac{1,903-0,699}{0,301}=4$$
